|
Память человека часто является ассоциативной; один предмет
напоминает нам о другом, а другой — о третьем. Если выпустить наши
мысли из-под контроля, они будут перемещаться от предмета к предмету
по цепочке умственных ассоциаций. Кроме
того, возможно использование ассоциативного мышления для
восстановления забытых образов. Если мы забыли, где оставили свои
очки, то пытаемся вспомнить, где видели их в последний раз, с кем в
это время разговаривали и что делали. Так устанавливается конец
цепочки ассоциаций, и это позволяет нашей
памяти соединять ассоциации для получения требуемого образа.
Ассоциативная память, рассмотренная в
предыдущих лекциях, является, строго говоря, автоассоциативной: это
означает, что образ может быть завершен или исправлен, но не может
быть ассоциирован с другим образом. Данный факт является результатом
одноуровневой структуры ассоциативной памяти, в ней вектор появляется на выходе тех
же нейронов, на которые поступает входной вектор.
Двунаправленная ассоциативная память
(ДАП) является гетероассоциативной; входной вектор поступает
на один набор нейронов, а соответствующий выходной вектор появляется
на другом наборе нейронов. Как и сеть Хопфилда, ДАП способна к обобщению, вырабатывая
правильные реакции, несмотря на искаженные входы. Кроме того, могут
быть реализованы адаптивные версии ДАП,
выделяющие эталонный образ из зашумленных экземпляров. Эти
возможности сильно напоминают процесс мышления человека и позволяют
искусственным нейронным сетям приблизиться к моделированию
естественного мозга.
Структура ДАП
На рис.
10.1 приведена базовая конфигурация ДАП. Она выбрана таким образом, чтобы
подчеркнуть сходство с сетями Хопфилда и предусмотреть увеличения
количества слоев. На рис.
10.1 входной вектор 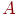 обрабатывается матрицей весов
обрабатывается матрицей весов 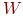 сети, в результате чего вырабатывается вектор выходных сигналов
нейронов
сети, в результате чего вырабатывается вектор выходных сигналов
нейронов  . Вектор . Вектор  затем обрабатывается транспонированной матрицей
затем обрабатывается транспонированной матрицей  весов сети, которая вырабатывает новые выходные сигналы,
представляющие собой новый входной вектор весов сети, которая вырабатывает новые выходные сигналы,
представляющие собой новый входной вектор 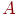 .
Процесс повторяется до тех пор, пока сеть не достигнет стабильного
состояния, в котором ни вектор .
Процесс повторяется до тех пор, пока сеть не достигнет стабильного
состояния, в котором ни вектор 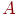 ,
ни вектор ,
ни вектор  не изменяются. Заметим, что нейроны в слоях 1 и 2
функционируют, как и в других парадигмах, вычисляя сумму взвешенных
входов и вычисляя по ней значение функции активации не изменяются. Заметим, что нейроны в слоях 1 и 2
функционируют, как и в других парадигмах, вычисляя сумму взвешенных
входов и вычисляя по ней значение функции активации  .
Этот процесс может быть выражен следующим образом: .
Этот процесс может быть выражен следующим образом:

или в векторной форме: 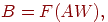
где  — вектор выходных сигналов нейронов слоя 2, — вектор выходных сигналов нейронов слоя 2, 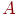 — вектор выходных сигналов нейронов слоя 1,
— вектор выходных сигналов нейронов слоя 1, 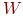 — матрица весов связей между слоями 1 и 2,
— матрица весов связей между слоями 1 и 2,  — функция активации.
— функция активации.
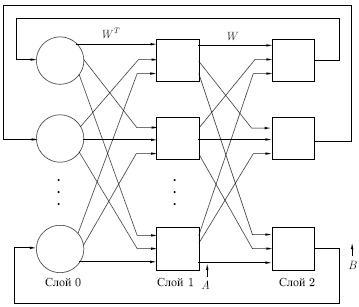
Рис. 10.1.
Аналогично, 
где  является транспозицией матрицы
является транспозицией матрицы 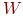 . .
Как отмечено нами ранее, Гроссберг показал преимущества
использования сигмоидальной (логистической) функции активации

где 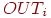 —
выход нейрона —
выход нейрона  , ,
 — взвешенная сумма входных сигналов нейрона — взвешенная сумма входных сигналов нейрона  , ,
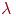 — константа, определяющая степень кривизны. — константа, определяющая степень кривизны.
В простейших версиях ДАП значение
константы 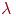 выбирается большим, в результате чего функция активации приближается
к простой пороговой функции. В дальнейшем будем предполагать, что
используется пороговая функция активации.
выбирается большим, в результате чего функция активации приближается
к простой пороговой функции. В дальнейшем будем предполагать, что
используется пороговая функция активации.
Примем также, что существует память
внутри каждого нейрона в слоях 1 и 2 и что выходные сигналы нейронов
изменяются одновременно с каждым тактом синхронизации, оставаясь
постоянными в паузах между этими тактами. Таким образом, поведение
нейронов может быть описано следующими правилами:
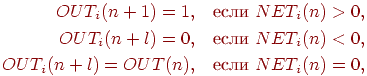
где  представляет собой величину выходного сигнала нейрона
представляет собой величину выходного сигнала нейрона  в момент времени
в момент времени  . .
Заметим, что, как и в описанных ранее сетях, слой 0 не производит
вычислений и не имеет памяти; он является
только средством распределения выходных сигналов слоя 2 к элементам
матрицы  . .
Восстановление запомненных ассоциаций
Долговременная память (или ассоциации) реализуется в весовых массивах 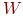 и
и  .
Каждый образ состоит из двух векторов: вектора .
Каждый образ состоит из двух векторов: вектора 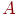 ,
являющегося выходом слоя 1, и вектора ,
являющегося выходом слоя 1, и вектора  ,
ассоциированного образа, являющегося выходом слоя 2. Для
восстановления ассоциированного образа вектор ,
ассоциированного образа, являющегося выходом слоя 2. Для
восстановления ассоциированного образа вектор 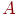 или его часть кратковременно устанавливаются на выходах слоя 1.
Затем вектор
или его часть кратковременно устанавливаются на выходах слоя 1.
Затем вектор 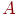 удаляется, и сеть приводится в стабильное состояние, вырабатывая
ассоциированный вектор
удаляется, и сеть приводится в стабильное состояние, вырабатывая
ассоциированный вектор  на выходе слоя 2. Далее вектор
на выходе слоя 2. Далее вектор  воздействует через транспонированную матрицу
воздействует через транспонированную матрицу  , воспроизводя воздействие исходного входного вектора , воспроизводя воздействие исходного входного вектора 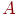 на выходе слоя 1. Каждый такой цикл вызывает уточнение выходных
векторов слоя 1 и 2 до тех пор, пока не будет достигнута точка
стабильности в сети. Эта точка может быть определена как
резонансная, поскольку вектор передается обратно и вперед между
слоями сети, всегда обрабатывая текущие выходные сигналы, но больше
не изменяя их. Состояние нейронов представляет собой кратковременную
память (КП), так как оно может быстро
изменяться при появлении другого входного вектора. Значения
коэффициентов весовой матрицы образуют долговременную память и могут изменяться только на более
длительном отрезке времени с помощью методов, представленных ниже в
данной лекции.
на выходе слоя 1. Каждый такой цикл вызывает уточнение выходных
векторов слоя 1 и 2 до тех пор, пока не будет достигнута точка
стабильности в сети. Эта точка может быть определена как
резонансная, поскольку вектор передается обратно и вперед между
слоями сети, всегда обрабатывая текущие выходные сигналы, но больше
не изменяя их. Состояние нейронов представляет собой кратковременную
память (КП), так как оно может быстро
изменяться при появлении другого входного вектора. Значения
коэффициентов весовой матрицы образуют долговременную память и могут изменяться только на более
длительном отрезке времени с помощью методов, представленных ниже в
данной лекции.
Сеть функционирует в направлении минимизации функции энергии
Ляпунова в основном таким же образом, как и сети Хопфилда в процессе
сходимости. Следовательно, каждый цикл модифицирует систему в
направлении энергетического минимума, расположение которого
определяется значениями весов.
Этот процесс может быть визуально представлен в форме
направленного движения мяча по резиновой ленте, вытянутой над
столом, причем каждому запомненному образу соответствует точка,
"вдавленная" в направлении поверхности стола. Рис.
10.2 иллюстрирует данную аналогию, на нем отмечен один
запомненный образ. Данный процесс формирует минимум гравитационной
энергии в каждой точке, соответствующей запомненному образу, с
соответствующим искривлением поля притяжения в направлении к данной
точке. Свободно движущийся мяч попадает в поле притяжения и в
результате будет двигаться в направлении энергетического минимума,
где и остановится.
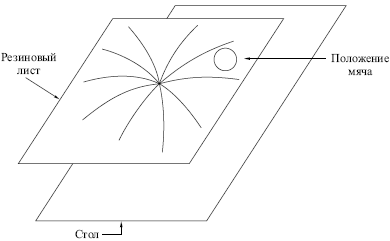
Рис. 10.2.
Кодировка ассоциаций
Обычно сеть обучается распознаванию множества образов. Обучение
производится с использованием обучающего набора, состоящего из пар
векторов 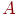 и и  .
Процесс обучения реализуется в форме вычислений; это означает, что
весовая матрица вычисляется как сумма произведений всех векторных
пар обучающего набора. B символьной форме запишем .
Процесс обучения реализуется в форме вычислений; это означает, что
весовая матрица вычисляется как сумма произведений всех векторных
пар обучающего набора. B символьной форме запишем
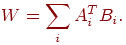
Предположим, что все запомненные образы представляют собой
двоичные векторы. Это ограничение будет выглядеть менее строгим,
если вспомнить, что все содержимое Библиотеки Университета может
быть закодировано в один очень длинный двоичный вектор. Показано,
что более высокая производительность достигается при использовании
биполярных векторов. При этом векторная компонента, большая чем 0,
становится  , а компонента, меньшая или равная 0, становится , а компонента, меньшая или равная 0, становится  . .
Предположим, что требуется обучить сеть с целью запоминания трех
пар двоичных векторов, причем векторы  имеют размерность такую же, как и векторы имеют размерность такую же, как и векторы  . Надо отметить, что это не является необходимым условием
для работы алгоритма; ассоциации могут
быть сформированы и между векторами различной размерности. . Надо отметить, что это не является необходимым условием
для работы алгоритма; ассоциации могут
быть сформированы и между векторами различной размерности.
| Исходный вектор |
Ассоциированный вектор |
Бинарная версия |
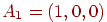 |
 |
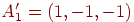 |
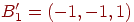 |
 |
 |
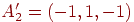 |
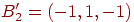 |
 |
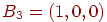 |
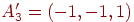 |
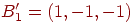 |
Вычисляем весовую матрицу: 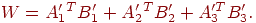

Далее, прикладывая входной вектор 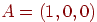 ,
вычисляем выходной вектор ,
вычисляем выходной вектор  : :
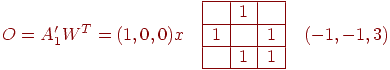
Используя пороговое правило,  , если , если  , ,  , если , если 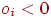 , ,  , не изменяется, если , не изменяется, если  , ,
вычисляем 
что является требуемой ассоциацией.
Затем, подавая вектор  через обратную связь на вход первого слоя к через обратную связь на вход первого слоя к  , получаем , получаем
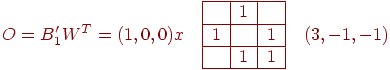
что дает значение  после применения пороговой функции и образует величину
вектора после применения пороговой функции и образует величину
вектора 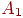 . .
Этот пример показывает, как входной вектор 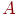 с использованием матрицы
с использованием матрицы 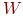 производит выходной вектор
производит выходной вектор  .
В свою очередь, вектор .
В свою очередь, вектор  с использованием матрицы
с использованием матрицы  производит вектор производит вектор 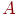 ,
и таким образом в системе формируется устойчивое состояние и
резонанс. ,
и таким образом в системе формируется устойчивое состояние и
резонанс.
ДАП обладает способностью к обобщению.
Например, если незавершенный или частично искаженный вектор подается
в качестве 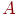 ,
сеть имеет тенденцию к выработке запомненного вектора ,
сеть имеет тенденцию к выработке запомненного вектора  ,
который, в свою очередь, стремится исправить ошибки в ,
который, в свою очередь, стремится исправить ошибки в 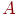 .
Возможно, для этого потребуется несколько проходов, но сеть сходится
к воспроизведению ближайшего запомненного образа. .
Возможно, для этого потребуется несколько проходов, но сеть сходится
к воспроизведению ближайшего запомненного образа.
Системы с обратной связью могут иметь тенденцию к колебаниям; это
означает, что они могут переходить от состояния к состоянию, никогда
не достигая стабильности. Доказано, что все ДАП безусловно стабильны при любых значениях
весов сети. Это важное свойство возникает из отношения
транспонирования между двумя весовыми матрицами и означает, что
любой набор ассоциаций может быть
использован без риска возникновения нестабильности.
Существует взаимосвязь между ДАП и
рассмотренными на предыдущих лекциях сетями Хопфилда. Если весовая
матрица 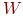 является квадратной и симметричной, то является квадратной и симметричной, то 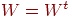 . В этом случае, если слои 1 и 2 являются одним и тем же
набором нейронов, ДАП превращается в
автоассоциативную сеть Хопфилда. . В этом случае, если слои 1 и 2 являются одним и тем же
набором нейронов, ДАП превращается в
автоассоциативную сеть Хопфилда.
Емкость памяти
Как и сети Хопфилда, ДАП имеет
ограничения на максимальное количество ассоциаций, которые она может точно
воспроизвести. Если этот лимит превышен, сеть может выработать
неверный выходной сигнал, воспроизводя ассоциации, которым не обучена.
Б. Коско получил оценки, в соответствии с которыми количество
запомненных ассоциаций не может превышать
количества нейронов в меньшем слое. Для этого емкость памяти должна быть максимизирована посредством
специального кодирования, при котором количество компонент со
значениями  равно количеству компонент со значениями
равно количеству компонент со значениями  в каждом биполярном векторе. Эта оценка оказалась слишком
оптимистичной. Е.Г. Рознер показал, что оценка емкости сетей
Хопфилда может быть легко обобщена для ДАП. Можно показать, что если
в каждом биполярном векторе. Эта оценка оказалась слишком
оптимистичной. Е.Г. Рознер показал, что оценка емкости сетей
Хопфилда может быть легко обобщена для ДАП. Можно показать, что если 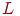 векторов выбраны случайно и представлены в указанной выше форме, и
если
векторов выбраны случайно и представлены в указанной выше форме, и
если 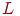 меньше чем меньше чем 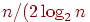 ), где ), где
 — количество нейронов в наименьшем слое, тогда все запомненные
образы, за исключением "малой части", могут быть восстановлены.
Например, если
— количество нейронов в наименьшем слое, тогда все запомненные
образы, за исключением "малой части", могут быть восстановлены.
Например, если  , тогда , тогда 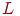 должно быть меньше 51. Если должны восстанавливаться все образы, то
должно быть меньше 51. Если должны восстанавливаться все образы, то
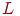 должно быть меньше
должно быть меньше  , то
есть меньше 25. Эти несколько озадачивающие результаты показывают,
что большие системы могут запоминать только умеренное количество
ассоциаций. , то
есть меньше 25. Эти несколько озадачивающие результаты показывают,
что большие системы могут запоминать только умеренное количество
ассоциаций.
Известно, что ДАП может иметь до  стабильных состояний, если пороговое значение стабильных состояний, если пороговое значение  выбирается для каждого нейрона. Такая конфигурация, которую авторы
назвали негомогенной ДАП, является
расширением исходной гомогенной ДАП, где
все пороги были нулевыми. Модифицированная передаточная функция
нейрона принимает в этом случае следующий вид:
выбирается для каждого нейрона. Такая конфигурация, которую авторы
назвали негомогенной ДАП, является
расширением исходной гомогенной ДАП, где
все пороги были нулевыми. Модифицированная передаточная функция
нейрона принимает в этом случае следующий вид:
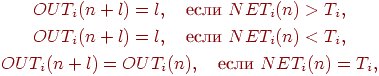
где 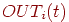 —
выход нейрона i в момент времени —
выход нейрона i в момент времени 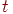 . .
С помощью выбора соответствующего порога для каждого нейрона,
количество стабильных состояний может быть сделано любым в диапазоне
от 1 до  , где , где  — количество нейронов в меньшем слое. К сожалению, эти состояния не
могут быть выбраны случайно; они определяются жесткой геометрической
процедурой. Если пользователь выбирает
— количество нейронов в меньшем слое. К сожалению, эти состояния не
могут быть выбраны случайно; они определяются жесткой геометрической
процедурой. Если пользователь выбирает 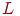 состояний случайным образом, причем
состояний случайным образом, причем 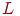 меньше
меньше ![(0,68)n^2/{[\log_2(n)] +
4}^2](beae9f27216dab5ec8f836dd2ce2b280.png) , и
если каждый вектор имеет , и
если каждый вектор имеет  компонент, равных +1, и остальные, равные
компонент, равных +1, и остальные, равные  , то можно сконструировать негомогенную ДАП, имеющую 98% этих векторов в качестве
стабильных состояний. Например, если , то можно сконструировать негомогенную ДАП, имеющую 98% этих векторов в качестве
стабильных состояний. Например, если  , то , то
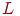 должно быть меньше 3637, а это является существенным улучшением по
сравнению с гомогенными ДАП, но намного
меньше, чем
должно быть меньше 3637, а это является существенным улучшением по
сравнению с гомогенными ДАП, но намного
меньше, чем  возможных состояний. возможных состояний.
Ограничение количества единиц во входных векторах представляет
серьезную проблему, тем более, что теория, которая позволяет
перекодировать произвольный набор векторов в такой "разреженный"
набор, отсутствует. Возможно, однако, что еще более серьезной
является проблема некорректной сходимости. Суть этой проблемы
заключается в том, что сеть может не производить точных ассоциаций вследствие природы поля притяжения;
об ее форме известно очень немногое. Это означает, что ДАП не является ассоциатором по отношению к
ближайшему соседнему образу. В действительности она может
производить ассоциации, имеющие слабое
отношение ко входному вектору. Как и в случае гомогенных ДАП, могут встречаться ложные стабильные
состояния, а об их количестве и природе известно крайне мало.
Несмотря на эти проблемы, ДАП остается
объектом интенсивных исследований. Основная привлекательность ДАП заключается в ее простоте. Кроме того, она
может быть реализована в виде СБИС (либо аналоговых, либо цифровых),
что делает ее потенциально недорогой. Так как наши знания постоянно
растут, ограничения ДАП могут быть сняты.
В этом случае как в экспериментальных, так и в практических
приложениях ДАП будет являться весьма
перспективным и полезным классом искусственных нейронных сетей.
Непрерывная ДАП
В предшествующем обсуждении нейроны в слоях 1 и 2 рассматривались
как синхронные; каждый нейрон обладает памятью, причем все нейроны изменяют состояния
одновременно под воздействием импульса от центральных часов. В
асинхронной системе любой нейрон свободен изменять состояние в любое
время, когда его вход предписывает это сделать.
Кроме того, при определении функции активации нейрона
использовался простой порог, образуя разрывность передаточной
функции нейронов. Как синхронность функционирования, так и
разрывность функций являются биологически неправдоподобными и совсем
необязательными; непрерывные асинхронные ДАП отвергают синхронность и разрывность, но
функционируют в основном аналогично дискретным версиям. Может
показаться, что такие системы должны быть нестабильными. Показано,
что непрерывные ДАП являются стабильными
(однако для них справедливы ограничения емкости, указанные ранее).
С. Гроссберг показал, что сигмоида является оптимальной функцией
активации благодаря ее способности усиливать низкоуровневые сигналы
и в то же время сжимать динамический диапазон нейронов. Непрерывная
ДАП может иметь сигмоидальную функцию с
величиной 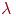 ,
близкой к единице, и создавать тем самым нейроны с плавной и
непрерывной реакцией, во многом аналогичной реакции их биологических
прототипов. ,
близкой к единице, и создавать тем самым нейроны с плавной и
непрерывной реакцией, во многом аналогичной реакции их биологических
прототипов.
Адаптивная ДАП
В версиях ДАП, рассматриваемых до сих
пор, весовая матрица вычисляется в виде суммы произведений пар
векторов. Такие вычисления полезны, поскольку они демонстрируют
функции, которые может выполнять ДАП.
Однако это определенно не тот способ, посредством которого
производится определение весов нейронов мозга.
Адаптивная ДАП изменяет свои веса в
процессе функционирования. Это означает, что подача на вход сети
обучающего набора входных векторов заставляет ее изменять
энергетическое состояние до получения резонанса. Постепенно
кратковременная память превращается в
долговременную память, настраивая сеть в
ходе ее функционирования. В процессе обучения векторы подаются на
слой 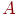 , а ассоциированные векторы — на слой , а ассоциированные векторы — на слой  .
Один из них или оба вектора могут быть зашумленными версиями
эталона; сеть обучается исходным векторам, свободным от шума. В этом
случае она извлекает сущность ассоциаций,
обучаясь эталонам, хотя "видела" только зашумленные
аппроксимации. .
Один из них или оба вектора могут быть зашумленными версиями
эталона; сеть обучается исходным векторам, свободным от шума. В этом
случае она извлекает сущность ассоциаций,
обучаясь эталонам, хотя "видела" только зашумленные
аппроксимации.
Так как доказано, что непрерывная ДАП
является стабильной независимо от значения весов, ожидается, что
медленное изменение ее весов не должно нарушить этой
стабильности.
Простейший обучающий алгоритм использует правило Хэбба, в котором
изменение веса пропорционально уровню активации его нейрона-
источника и уровню активации нейрона-приемника. В символьной записи
это выглядит следующим образом: 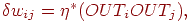
где  —
изменение веса связи нейрона —
изменение веса связи нейрона  с нейроном
с нейроном 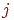 в матрицах
в матрицах 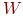 или
или  , , 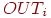 — выход нейрона — выход нейрона  слоя 1 или 2,
слоя 1 или 2, 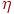 — положительный нормирующий коэффициент обучения, меньший
1. — положительный нормирующий коэффициент обучения, меньший
1.
Конкурирующая ДАП
Во многих конкурирующих нейронных системах наблюдаются некоторые
виды конкуренции между нейронами. В нейронах, обрабатывающих сигналы
от сетчатки, латеральное торможение приводит к увеличению выхода
наиболее высокоактивных нейронов за счет соседних. Такие системы
увеличивают контрастность, поднимая уровень активности нейронов,
подсоединенных к яркой области сетчатки, и в то же время еще более
ослабляя выходы нейронов, подсоединенных к темным областям. В ДАП конкуренция реализуется с помощью взаимного
соединения нейронов внутри каждого слоя посредством дополнительных
связей. Веса этих связей формируют другую весовую матрицу с
положительными значениями элементов главной диагонали и
отрицательными значениями остальных элементов. Теорема
Кохонена-Гроссберга показывает, что такая сеть является безусловно
стабильной, если весовые матрицы симметричны. На практике сети
обычно стабильны даже в случае отсутствия симметрии весовых матриц.
Однако неизвестно, какие особенности весовых матриц могут привести к
неустойчивости функционирования сети.
|




