|
APT представляет собой нечто большее,
чем философия, но намного менее конкретное, чем программа для
компьютера. Поэтому возник широкий круг реализаций, сохраняющих идеи
APT, но сильно отличающихся в деталях.
Описываемая далее реализация может рассматриваться в качестве
типовой, но необходимо иметь в виду, что другие успешные реализации
имеют большие отличия от нее.
Функционирование сетей APT
Рассмотрим более детально пять фаз процесса функционирования
APT: инициализацию, распознавание,
сравнение, поиск и обучение.
Инициализация. Перед началом процесса обучения сети все
весовые векторы 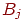 и и 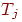 , а также параметр сходства , а также параметр сходства 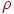 , должны быть установлены в начальные значения. , должны быть установлены в начальные значения.
Веса векторов 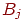 все инициализируются в одинаковые малые значения. Эти
значения должны удовлетворять условию все инициализируются в одинаковые малые значения. Эти
значения должны удовлетворять условию
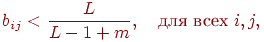
где  — количество компонент входного вектора, — количество компонент входного вектора, 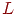 — константа, большая 1 (обычно
— константа, большая 1 (обычно  ). ).
Эта величина является критической; если она слишком большая, сеть
может распределить все нейроны распознающего слоя одному входному
вектору.
Веса векторов 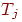 все инициализируются в единичные значения, так что все инициализируются в единичные значения, так что 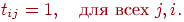
Эти значения также являются критическими; показано, что слишком
маленькие веса приводят к отсутствию соответствия в слое сравнения и
отсутствию обучения.
Параметр сходства 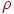 устанавливается в диапазоне от 0 до 1 в зависимости от
требуемой степени сходства между запомненным образом и входным
вектором. При высоких значениях устанавливается в диапазоне от 0 до 1 в зависимости от
требуемой степени сходства между запомненным образом и входным
вектором. При высоких значениях 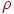 сеть относит к одному классу только очень слабо
отличающиеся образы. С другой стороны, малое значение сеть относит к одному классу только очень слабо
отличающиеся образы. С другой стороны, малое значение 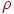 заставляет сеть группировать образы, которые имеют слабое
сходство между собой. Для выработки точной классификации полезна
возможность изменять коэффициент сходства на протяжении процесса
обучения, обеспечивая только грубую классификацию в начале процесса
обучения и затем постепенно увеличивая коэффициент сходства.
Распознавание. Появление на входе сети входного вектора заставляет сеть группировать образы, которые имеют слабое
сходство между собой. Для выработки точной классификации полезна
возможность изменять коэффициент сходства на протяжении процесса
обучения, обеспечивая только грубую классификацию в начале процесса
обучения и затем постепенно увеличивая коэффициент сходства.
Распознавание. Появление на входе сети входного вектора  инициализирует фазу распознавания. Так как вначале выходной вектор
слоя распознавания отсутствует, сигнал
инициализирует фазу распознавания. Так как вначале выходной вектор
слоя распознавания отсутствует, сигнал  устанавливается в 1 функцией ИЛИ вектора
устанавливается в 1 функцией ИЛИ вектора  ,
обеспечивая все нейроны слоя сравнения одним из двух входов,
необходимых для их возбуждения (как требует правило двух третей). В
результате любая компонента вектора ,
обеспечивая все нейроны слоя сравнения одним из двух входов,
необходимых для их возбуждения (как требует правило двух третей). В
результате любая компонента вектора  ,
равная единице, обеспечивает второй единичный вход, заставляя
соответствующий нейрон слоя сравнения возбуждаться и устанавливая
его выход в единицу. Таким образом, в этот момент времени вектор ,
равная единице, обеспечивает второй единичный вход, заставляя
соответствующий нейрон слоя сравнения возбуждаться и устанавливая
его выход в единицу. Таким образом, в этот момент времени вектор
 идентичен вектору
идентичен вектору  . .
Как обсуждалось ранее, распознавание реализуется вычислением
свертки для каждого нейрона слоя распознавания, определяемой
следующим выражением: 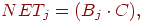
где 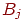 —
весовой вектор, соответствующий нейрону —
весовой вектор, соответствующий нейрону 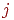 в слое распознавания,
в слое распознавания,  — выходной вектор нейронов слоя сравнения (в этот момент
— выходной вектор нейронов слоя сравнения (в этот момент  равно
равно  ), ), 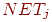 — возбуждение нейрона — возбуждение нейрона 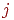 в слое распознавания.
в слое распознавания.
 является пороговой функцией, определяемой следующим
образом: является пороговой функцией, определяемой следующим
образом:
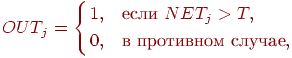
где  представляет собой порог. представляет собой порог.
Принято, что латеральное торможение существует, но игнорируется
здесь для сохранения простоты выражения. Торможение является
причиной того, что только нейрон с максимальным значением NET будет
иметь выход, равный единице; все остальные нейроны будут иметь
нулевой выход. Можно рассмотреть системы, в которых в распознающем
слое возбуждаются несколько нейронов в каждый момент времени, однако
это выходит за рамки данной работы.
Сравнение. На этой фазе сигнал обратной связи от слоя
распознавания устанавливает  в нуль; правило двух третей позволяет возбуждаться только тем
нейронам, которые имеют соответствующие компоненты векторов
в нуль; правило двух третей позволяет возбуждаться только тем
нейронам, которые имеют соответствующие компоненты векторов  и
и  , равные единице. , равные единице.
Блок сброса сравнивает вектор  и входной вектор
и входной вектор  ,
вырабатывая сигнал сброса, когда их сходство ,
вырабатывая сигнал сброса, когда их сходство  ниже порога сходства. Вычисление этого сходства упрощается тем, что
оба вектора являются двоичными (все элементы либо 0, либо 1).
Следующая процедура проводит требуемое вычисление сходства:
ниже порога сходства. Вычисление этого сходства упрощается тем, что
оба вектора являются двоичными (все элементы либо 0, либо 1).
Следующая процедура проводит требуемое вычисление сходства:
- Вычислить
 — количество единиц в векторе — количество единиц в векторе  . .
- Вычислить
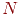 — количество единиц в векторе — количество единиц в векторе  . .
Затем вычислить сходство  следующим образом:
следующим образом: 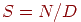 . .
Например, примем, что
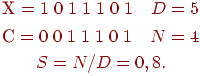
 может изменяться от 1 (наилучшее соответствие) до 0
(наихудшее соответствие). может изменяться от 1 (наилучшее соответствие) до 0
(наихудшее соответствие).
Заметим, что правило двух третей делает  логическим произведением входного вектора
логическим произведением входного вектора 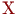 и вектора
и вектора  . Однако . Однако  равен
равен 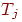 ,
весовому вектору выигравшего соревнование нейрона. Таким образом, ,
весовому вектору выигравшего соревнование нейрона. Таким образом,
 может быть определено как количество единиц в логическом
произведении векторов
может быть определено как количество единиц в логическом
произведении векторов 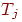 и и  . .
Поиск. Если сходство  выигравшего нейрона превышает параметр сходства, поиск не требуется.
Однако если сеть предварительно была обучена, появление на входе
вектора, не идентичного ни одному из предъявленных ранее, может
возбудить в слое распознавания нейрон со сходством ниже требуемого
уровня. В соответствии с алгоритмом обучения возможно, что другой
нейрон в слое распознавания будет обеспечивать более хорошее
соответствие, превышая требуемый уровень сходства, несмотря на то,
что свертка между его весовым вектором и входным вектором может
иметь меньшее значение. Пример такой ситуации показан ниже.
выигравшего нейрона превышает параметр сходства, поиск не требуется.
Однако если сеть предварительно была обучена, появление на входе
вектора, не идентичного ни одному из предъявленных ранее, может
возбудить в слое распознавания нейрон со сходством ниже требуемого
уровня. В соответствии с алгоритмом обучения возможно, что другой
нейрон в слое распознавания будет обеспечивать более хорошее
соответствие, превышая требуемый уровень сходства, несмотря на то,
что свертка между его весовым вектором и входным вектором может
иметь меньшее значение. Пример такой ситуации показан ниже.
Если сходство ниже требуемого уровня, запомненные образы могут
быть просмотрены, чтобы найти образ, наиболее соответствующий
входному вектору. Если такой образ отсутствует, вводится новый
несвязанный нейрон, который в дальнейшем будет обучен. Чтобы
инициализировать поиск, сигнал сброса тормозит возбужденный нейрон в
слое распознавания на время проведения поиска, сигнал  устанавливается в единицу и другой нейрон в слое распознавания
выигрывает соревнование. Его запомненный образ затем проверяется на
сходство, и процесс повторяется до тех пор, пока конкуренцию не
выиграет нейрон из слоя распознавания со сходством, большим
требуемого уровня (успешный поиск), либо пока все связанные нейроны
не будут проверены и заторможены (неудачный поиск).
устанавливается в единицу и другой нейрон в слое распознавания
выигрывает соревнование. Его запомненный образ затем проверяется на
сходство, и процесс повторяется до тех пор, пока конкуренцию не
выиграет нейрон из слоя распознавания со сходством, большим
требуемого уровня (успешный поиск), либо пока все связанные нейроны
не будут проверены и заторможены (неудачный поиск).
Неудачный поиск будет автоматически завершаться на несвязанном
нейроне, так как его веса все равны единице, своему начальному
значению. Поэтому правило двух третей приведет к идентичности
вектора  входному вектору входному вектору  ,
сходство ,
сходство  примет значение единицы и критерий сходства будет
удовлетворен. примет значение единицы и критерий сходства будет
удовлетворен.
Обучение. Обучение представляет собой процесс, в котором
набор входных векторов подается последовательно на вход сети, а веса
сети изменяются при этом таким образом, чтобы сходные векторы
активизировали соответствующие им нейроны. Заметим, что это -
неуправляемое обучение, здесь нет учителя и нет целевого вектора,
определяющего требуемый ответ.
Различают два вида обучения: медленное и быстрое. При медленном
обучении входной вектор предъявляется настолько кратковременно, что
веса сети не успевают достигнуть своих ассимптотических значений при
единичном предъявлении. В этом случае значения весов будут
определяться, скорее, статистическими характеристиками входных
векторов, чем характеристиками какого-то одного входного вектора.
Динамика сети в процессе медленного обучения описывается
дифференциальными уравнениями.
Быстрое обучение является специальным случаем медленного
обучения, когда входной вектор прикладывается на достаточно
длительный срок, чтобы позволить весам приблизиться к их
окончательным значениям. В этом случае процесс обучения описывается
только алгебраическими выражениями. Кроме того, компоненты весовых
векторов 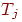 принимают двоичные значения, в отличие от непрерывного диапазона
значений, требуемого в случае быстрого обучения. В данной лекции мы
опишем только быстрое обучение.
принимают двоичные значения, в отличие от непрерывного диапазона
значений, требуемого в случае быстрого обучения. В данной лекции мы
опишем только быстрое обучение.
Рассмотренный далее обучающий алгоритм используется как в случае
успешного, так и в случае неуспешного поиска.
Пусть вектор весов 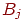 (связанный с возбужденным нейроном (связанный с возбужденным нейроном 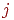 распознающего слоя) равен нормализованной величине вектора
распознающего слоя) равен нормализованной величине вектора  .
Эти веса вычисляются следующим образом: .
Эти веса вычисляются следующим образом:
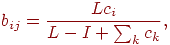
где  — —  -я компонента выходного вектора слоя сравнения, -я компонента выходного вектора слоя сравнения, 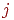 — номер выигравшего нейрона в слое распознавания,
— номер выигравшего нейрона в слое распознавания,  — вес связи, соединяющей нейрон — вес связи, соединяющей нейрон  в слое сравнения с нейроном
в слое сравнения с нейроном 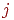 в слое распознавания,
в слое распознавания, 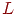 — константа > 1 (обычно 2).
— константа > 1 (обычно 2).
Компоненты вектора весов 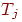 , связанного с новым запомненным вектором, изменяются таким
образом, что становятся равны соответствующим двоичным величинам
вектора , связанного с новым запомненным вектором, изменяются таким
образом, что становятся равны соответствующим двоичным величинам
вектора  : : 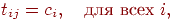
где  является весом связи между выигравшим нейроном
является весом связи между выигравшим нейроном 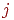 в слое распознавания и нейроном
в слое распознавания и нейроном  в слое сравнения.
в слое сравнения.
Пример обучения сети АРТ
В общих чертах сеть обучается при помощи изменения весов таким
образом, что предъявление входного вектора заставляет сеть
активизировать нейроны в слое распознавания, связанные со сходным
запомненным вектором. Кроме этого, обучение проводится в форме, не
разрушающей запомненные ранее образы, и предотвращает тем самым
временную нестабильность. Эта задача управляется на уровне выбора
критерия сходства. Новый входной образ (который сеть раньше не
видела) не будет соответствовать запомненным образам с точки зрения
параметра сходства, тем самым формируя новый запоминаемый образ.
Входной образ, в достаточной степени соответствующий одному из
запомненных образов, не будет формировать нового экземпляра, он
просто будет модифицировать тот, на который он похож. В результате
при соответствующем выборе критерия сходства предотвращается
запоминание ранее изученных образов и временная нестабильность.
На рис.
12.1 показан типичный сеанс обучения сети APT. Буквы изображены состоящими из маленьких
квадратов, каждая буква размерностью  . Каждый квадрат в левой части представляет компоненту
вектора . Каждый квадрат в левой части представляет компоненту
вектора  с единичным значением, не показанные квадраты являются
компонентами с нулевыми значениями. Буквы справа представляют
запомненные образы, каждый является набором величин компонент
вектора с единичным значением, не показанные квадраты являются
компонентами с нулевыми значениями. Буквы справа представляют
запомненные образы, каждый является набором величин компонент
вектора 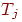 . .
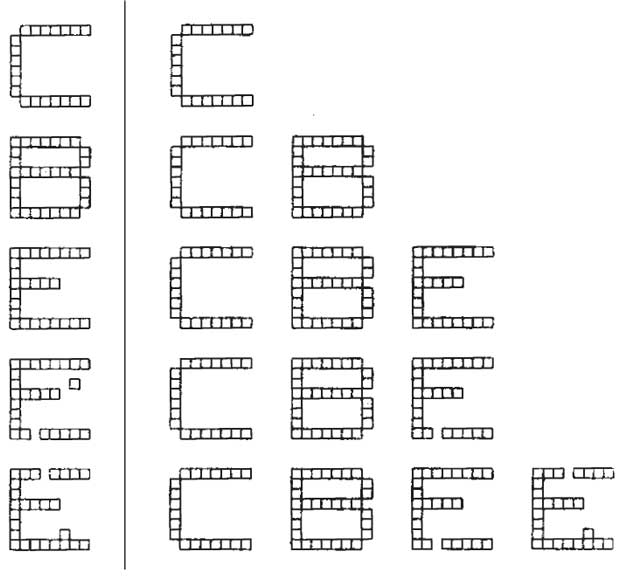
Рис. 12.1.
Вначале на вход заново проинициированной системы подается буква
"С". Так как отсутствуют запомненные образы, фаза поиска
заканчивается неуспешно; новый нейрон выделяется в слое
распознавания, и веса 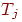 устанавливаются равными соответствующим компонентам
входного вектора, при этом веса устанавливаются равными соответствующим компонентам
входного вектора, при этом веса 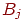 представляют масштабированную версию входного вектора. представляют масштабированную версию входного вектора.
Далее предъявляется буква "В". Она также вызывает неуспешное
окончание фазы поиска и выделение нового нейрона. Аналогичный
процесс повторяется для буквы "Е". Затем слабо искаженная версия
буквы "Е" подается на вход сети. Она достаточно точно соответствует
запомненной букве "Е", чтобы выдержать проверку на сходство, поэтому
используется для обучения сети. Отсутствующий пиксель в нижней ножке
буквы "Е" устанавливает в 0 соответствующую компоненту вектора  ,
заставляя обучающий алгоритм установить этот вес запомненного образа
в нуль, тем самым воспроизводя искажения в запомненном образе.
Дополнительный изолированный квадрат не изменяет запомненного
образа, так как не соответствует единице в запомненном образе. ,
заставляя обучающий алгоритм установить этот вес запомненного образа
в нуль, тем самым воспроизводя искажения в запомненном образе.
Дополнительный изолированный квадрат не изменяет запомненного
образа, так как не соответствует единице в запомненном образе.
Четвертым символом является буква "Е" с двумя различными
искажениями. Она не соответствует ранее запомненному образу ( меньше чем
меньше чем 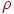 ), поэтому для ее запоминания выделяется новый нейрон. ), поэтому для ее запоминания выделяется новый нейрон.
Этот пример иллюстрирует важность выбора корректного значения
критерия сходства. Если значение критерия слишком велико,
большинство образов не будут подтверждать сходство с ранее
запомненными и сеть будет выделять новый нейрон для каждого из них.
Такой процесс приводит к плохому обобщению в сети, в результате даже
незначительные изменения одного образа будут создавать отдельные
новые категории; далее количество категорий увеличивается, все
доступные нейроны распределяются, и способность системы к восприятию
новых данных теряется. Наоборот, если критерий сходства слишком мал,
сильно различающиеся образы будут группироваться вместе, искажая
запомненный образ, до тех пор, пока в результате не получится очень
малое сходство с одним из них.
К сожалению, отсутствует теоретическое обоснование выбора
критерия сходства, и в каждом конкретном случае необходимо решить
"волевым усилием", какая степень сходства должна быть принята для
отнесения образов к одной категории. Границы между категориями часто
неясны, и решение задачи для большого набора входных векторов может
быть чрезмерно трудным.
Гроссберг предложил процедуру с использованием обратной связи для
настройки коэффициента сходства, вносящую, однако, некоторые
искажения в результаты классификации как "наказание" за внешнее
вмешательство с целью увеличения коэффициента сходства. Такие
системы требуют правил оценки корректности для производимой ими
классификации.
Характеристики АРТ
Системы APT имеют ряд важных
характеристик, не являющихся очевидными. Формулы и алгоритмы могут
казаться произвольными, в то время как в действительности они были
тщательно отобраны и соответствуют требованиям теорем относительно
производительности систем APT. В данном
разделе описываются некоторые алгоритмы APT, раскрывающие отдельные вопросы
инициализации и обучения.
Инициализация весовых векторов T
В ранее рассмотренном примере обучения сети можно было видеть,
что правило двух третей приводит к вычислению вектора  как функции И между входным вектором
как функции И между входным вектором  и выигравшим соревнование запомненным вектором
и выигравшим соревнование запомненным вектором 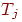 . Следовательно, любая компонента вектора . Следовательно, любая компонента вектора  будет равна единице в том случае, если соответствующие компоненты
обоих векторов равны единице. После обучения эти компоненты вектора
будет равна единице в том случае, если соответствующие компоненты
обоих векторов равны единице. После обучения эти компоненты вектора
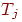 остаются единичными; все остальные устанавливаются в
нуль. остаются единичными; все остальные устанавливаются в
нуль.
Это объясняет, почему веса  должны инициализироваться единичными значениями. Если бы
они были проинициализированы нулевыми значениями, все компоненты
вектора должны инициализироваться единичными значениями. Если бы
они были проинициализированы нулевыми значениями, все компоненты
вектора  были бы нулевыми независимо от значений компонент входного
вектора, и обучающий алгоритм предохранял бы веса от изменения их
нулевых значений. были бы нулевыми независимо от значений компонент входного
вектора, и обучающий алгоритм предохранял бы веса от изменения их
нулевых значений.
Обучение может рассматриваться как процесс "сокращения" компонент
запомненных векторов, которые не соответствуют входным векторам.
Процесс необратим, если вес однажды установлен в нуль, — обучающий
алгоритм никогда не восстановит его единичное значение.
Это свойство имеет важное отношение к процессу обучения.
Предположим, что группа точно соответствующих векторов должна быть
классифицирована как одна категория, определяемая возбуждением
одного нейрона в слое распознавания. Если эти векторы
последовательно предъявляются сети, то при предъявлении первого
будет распределяться нейрон распознающего слоя и его веса будут
обучены с целью соответствия входному вектору. Обучение при
предъявлении остальных векторов будет приводить к обнулению весов в
тех позициях, которые имеют нулевые значения в любом из входных
векторов. Таким образом, запомненный вектор представляет собой
логическое пересечение всех обучающих векторов и может включать
существенные характеристики данной категории весов. Новый вектор,
включающий только существенные характеристики, будет соответствовать
этой категории. Таким образом, сеть корректно распознает образ,
никогда не виденный ранее, т. е. реализуется возможность,
напоминающая процесс восприятия в мозге человека.
Настройка весовых векторов Bj
Выражение, описывающее процесс настройки весов, является
центральным для описания процесса функционирования сетей APT:
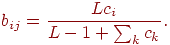
Сумма в знаменателе представляет собой количество единиц на
выходе слоя сравнения. Заданная величина может быть рассмотрена как
"размер" этого вектора. В такой интерпретации "большие" векторы  производят более маленькие величины весов
производят более маленькие величины весов  , чем "маленькие" вектора , чем "маленькие" вектора  .
Это свойство самомасштабирования делает возможным разделение двух
векторов в случае, когда один вектор является поднабором другого, т.
е. когда набор единичных компонент одного вектора составляет
подмножество единичных компонент другого. .
Это свойство самомасштабирования делает возможным разделение двух
векторов в случае, когда один вектор является поднабором другого, т.
е. когда набор единичных компонент одного вектора составляет
подмножество единичных компонент другого.
Чтобы проиллюстрировать проблему, которая возникает при
отсутствии масштабирования, используемого в данном выражении,
предположим, что сеть обучена двум приведенным ниже входным
векторам, при этом каждому распределен нейрон в слое
распознавания.
Заметим, что  является поднабором является поднабором 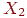 . В отсутствие свойства масштабирования веса . В отсутствие свойства масштабирования веса  и и  получат значения, идентичные значениям входных векторов.
Если начальные значения выбраны равными 1,0, веса образов будут
иметь следующие значения: если получат значения, идентичные значениям входных векторов.
Если начальные значения выбраны равными 1,0, веса образов будут
иметь следующие значения: если  прикладывается повторно, оба нейрона в слое распознавания получают
одинаковые активации; следовательно, нейрон 2 — ошибочный нейрон —
выиграет конкуренцию.
прикладывается повторно, оба нейрона в слое распознавания получают
одинаковые активации; следовательно, нейрон 2 — ошибочный нейрон —
выиграет конкуренцию.
Кроме выполнения некорректной классификации, может быть нарушен
процесс обучения. Так как 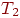 равно 1 1 1 0 0, только первая единица соответствует
единице входного вектора, и равно 1 1 1 0 0, только первая единица соответствует
единице входного вектора, и  устанавливается в 1 0 0 0 0; критерий сходства удовлетворяется и
алгоритм обучения устанавливает вторую и третью единицы векторов
устанавливается в 1 0 0 0 0; критерий сходства удовлетворяется и
алгоритм обучения устанавливает вторую и третью единицы векторов
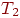 и и  в нуль, разрушая запомненный образ. в нуль, разрушая запомненный образ.
Масштабирование весов  позволяет избежать такого нежелательного течения событий.
Предположим, что используется значение позволяет избежать такого нежелательного течения событий.
Предположим, что используется значение  , тем самым определяя следующую формулу: , тем самым определяя следующую формулу:
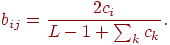
Подавая на вход сети вектор  , получим возбуждающее воздействие 1,0 для нейрона 1 в слое
распознавания и , получим возбуждающее воздействие 1,0 для нейрона 1 в слое
распознавания и 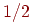 для нейрона 2; таким образом, нейрон 1 (правильный)
выиграет соревнование. Аналогично, предъявление вектора для нейрона 2; таким образом, нейрон 1 (правильный)
выиграет соревнование. Аналогично, предъявление вектора 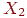 вызовет уровень возбуждения 1,0 для нейрона 1 и 3/2 для
нейрона 2, тем самым снова правильно выбирая победителя. вызовет уровень возбуждения 1,0 для нейрона 1 и 3/2 для
нейрона 2, тем самым снова правильно выбирая победителя.
Инициализация весов bij
Инициализация весов  малыми значениями является существенной для корректного
функционирования систем APT. Если они
слишком большие, входной вес вектора, который уже был запомнен,
станет скорее активизировать несвязанный нейрон, чем ранее
обученный. малыми значениями является существенной для корректного
функционирования систем APT. Если они
слишком большие, входной вес вектора, который уже был запомнен,
станет скорее активизировать несвязанный нейрон, чем ранее
обученный.
Установка этих весов в малые величины гарантирует, что
несвязанные нейроны не будут получать возбуждения большего, чем
обученные нейроны в слое распознавания. Используя предыдущий пример
с  , , 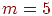 и и 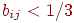 , произвольно установим , произвольно установим 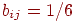 . С такими весами предъявление вектора, которому сеть была
ранее обучена, приведет к более высокому уровню активации для
правильно обученного нейрона в слое распознавания, чем для
несвязанного нейрона. Например, для несвязанного нейрона . С такими весами предъявление вектора, которому сеть была
ранее обучена, приведет к более высокому уровню активации для
правильно обученного нейрона в слое распознавания, чем для
несвязанного нейрона. Например, для несвязанного нейрона  будет производить возбуждение 1/6, в то время как будет производить возбуждение 1/6, в то время как 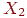 будет производить возбуждение 1/2; и то, и другое ниже
возбуждения для обученных нейронов. будет производить возбуждение 1/2; и то, и другое ниже
возбуждения для обученных нейронов.
Поиск. Может показаться, что в описанных алгоритмах
отсутствует необходимость фазы поиска, за исключением случая, когда
для входного вектора должен быть распределен новый несвязанный
нейрон. Это не совсем так: предъявление входного вектора, сходного,
но не абсолютно идентичного одному из запомненных образов, может при
первом испытании не обеспечить выбор нейрона слоя распознавания с
уровнем сходства, большим р, хотя такой нейрон будет существовать;
и, тем самым, без поиска не обойтись.
Как и в предыдущем примере, предположим, что сеть обучается
следующим двум векторам: 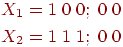
с векторами весов  , обученными следующим образом: , обученными следующим образом: 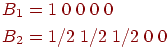
Теперь приложим входной вектор  . В
этом случае возбуждение нейрона 1 в слое распознавания будет 1,0, а
нейрона 2 только 2/3. Нейрон 1 выйдет победителем (хотя он не лучшим
образом соответствует входному вектору), вектор . В
этом случае возбуждение нейрона 1 в слое распознавания будет 1,0, а
нейрона 2 только 2/3. Нейрон 1 выйдет победителем (хотя он не лучшим
образом соответствует входному вектору), вектор  получит значение 1 1 0 0 0,
получит значение 1 1 0 0 0,  будет равно 1/2. Если уровень сходства установлен в 3/4, нейрон 1
будет заторможен и нейрон 2 выиграет состязание.
будет равно 1/2. Если уровень сходства установлен в 3/4, нейрон 1
будет заторможен и нейрон 2 выиграет состязание.  станет равным 1 1 0 0 0,
станет равным 1 1 0 0 0,  станет равным 1, критерий сходства будет удовлетворен, и поиск
закончится.
станет равным 1, критерий сходства будет удовлетворен, и поиск
закончится.
Теоремы APT
Гроссберг доказал некоторые теоремы, которые описывают
характеристики сетей APT. Четыре
результата, приведенные ниже, являются одними из наиболее
важных:
- После стабилизации процесса обучения предъявление одного из
обучающих векторов (или вектора с существенными характеристиками
категории) будет активизировать требуемый нейрон слоя
распознавания без поиска. Такая характеристика "прямого доступа"
обеспечивает быстрый доступ к предварительно изученным образам.
- Процесс поиска является устойчивым. После определения
выигравшего нейрона в сети не будет возбуждений других нейронов
из-за изменения векторов выхода слоя сравнения
 ; только сигнал сброса может вызвать такие изменения. ; только сигнал сброса может вызвать такие изменения.
- Процесс обучения является устойчивым. Обучение не будет
вызывать переключения с одного возбужденного нейрона слоя
распознавания на другой.
- Процесс обучения конечен. Любая последовательность
произвольных входных векторов будет производить стабильный набор
весов после конечного количества обучающих серий. Повторяющиеся
последовательности обучающих векторов не будут приводить к
циклическому изменению весов.
Дальнейшее развитие АРТ: архитектуры АРТ-2 и АРТ-3
Нерешенные проблемы и недостатки АРТ-1
Нейронные сети АРТ, при всех их
замечательных свойствах, имеют ряд недостатков. Один из них —
большое количество синаптических связей в сети, в расчете на единицу
запоминаемой информации. При этом многие из весов этих связей
(например, вектора  )
оказываются после обучения нулевыми. Эту особенность следует
учитывать при аппаратных реализациях. )
оказываются после обучения нулевыми. Эту особенность следует
учитывать при аппаратных реализациях.
Сеть АРТ-1 приспособлена к работе
только с битовыми векторами. Это неудобство преодолевается в сетях
АРТ-2 и АРТ-3.
Однако в этих архитектурах, равно как и в АРТ-1, сохраняется главный недостаток АРТ — локализованность памяти. Память нейросети
АРТ не является распределенной, и
некоторой заданной категории отвечает вполне конкретный нейрон слоя
распознавания. При его разрушении теряется память обо всей
категории. Эта особенность, увы, не позволяет говорить о сетях адаптивной резонансной теории как о прямых
моделях биологических нейронных сетей. Память последних является
распределенной.
Сети АРТ-2 и АРТ-3
Основной отличительной чертой нейронной сети АРТ-2 является возможность работы с
аналоговыми векторами и сигналами. По сравнению с АРТ-1 в архитектуре сети сделаны некоторые
изменения, позволяющие отдельным подсистемам функционировать
асинхронно, что является принципиальной необходимостью для
аппаратных реализаций.
Важное отличие аналоговых сигналов от битовых — принципиальная
возможность аналоговых векторов быть сколь угодно близкими друг к
другу (в то время как простанство битовых векторов дискретно). Это
накладывает дополнительные требования на функционирование нейронов
слоя сравнения: требуется более тонкий и чувствительный механизм для
выделения областей резонанса. Общим решением здесь является переход
к многослойной архитектуре, со все более точной настройкой при
переходе от слоя к слою, что и применено в АРТ-2. Функционирование слоя распознавания
принципиально не изменяется.
Сети АРТ-2 применялись для
распознавания движущихся изображений. Успешные эксперименты
проведены в Массачусетском Технологическом Институте (MIT).
Поскольку нейросистемы АРТ не содержат
механизма инвариантного распознавания (в отличие от неокогнитрона,
см. следующие лекции), то в сочетании с ними применяются
специализированные (часто не нейросетевые) системы инвариантного
представления образов, например, двумерное преобразование Фурье или
более сложные алгоритмы. Более подробное рассмотрение особенностей и
применений АРТ-2 требует
профессионального изучения и не входит в наши цели.
Следующим шагом в развитии АРТ явилась
сеть АРТ-3. Особенности обучения
нейронов сетей АРТ-1 и АРТ-2 не позволяют использовать эти сети в
качестве элементов более крупных иерархических нейросистем, в
частности, компоновать из них многослойные сети. Поэтому
представление в АРТ иерархически
организованной информации затруднительно, и это весьма отдаляет ее
от систем восприятия человека и животных.
Изложенные проблемы решены в сети АРТ-3, которая выступает как многослойная
архитектура. При переходе от слоя к слою происходит контрастирование
входных образов и запоминание их в виде все более общих категорий.
При этом основной задачей каждого отдельного слоя является сжатие
входящей информации. Образ входит в адаптирующийся резонанс между
некоторой парой слоев, в дальнейшем этот резонанс распространяется
на следующие слои иерархии. В АРТ-1 и
АРТ-2 недостаточный уровень резонанса
приводил к генерации сигнала сброса, что приводило к полному
торможению слоя распознавания. В случае многослойной сети АРТ-3 подобное недопустимо, так как при этом
разрывается поток информации. Поэтому в АРТ-3 введен специальный механизм — зависимость
активности синапсов обратных связей от времени, — аналогичный
рефрактерному торможению биологического нейрона после передачи
возбуждения. Поэтому вместо полного сброса сигнала происходит
торможение синаптических сигналов обратной связи, и слой сравнения
получает исходное состояние возбуждения для выполнения фазы поиска
нового резонанса.
Интересным предложением является также использование в
многослойной иерархии слоев, которые не являются слоями АРТ, а принадлежат некоторой другой
архитектуре. В этом случае система получается гибридной, что может
привести к возникновению новых полезных свойств.
Развитие теоретических исследований АРТ продолжается. По высказыванию авторов
теории, АРТ представляет собой нечто
существенно более конкретное, чем философское построение, но намного
менее конкретное, чем законченная программа для компьютера. Однако
уже в современном виде, опираясь на свою более чем 20-летнюю
историю, сети АРТ с успехом применяются в
различных областях. АРТ сделала также
важный шаг вперед в общей проблеме моделирования
пластично-стабильного восприятия.
|




