|
Люди решают сложные задачи распознавания
образов с обескураживающей легкостью. Двухлетний ребенок без
видимых усилий различает тысячи лиц и других объектов, составляющих
его окружение, несмотря на изменение расстояния, ракурса,
перспективы и освещения.
Может показаться, что изучение этих врожденных способностей
должно упростить задачу разработки компьютера, повторяющего
способности человека к распознаванию. Ничто не может быть более
далеким от истины. Сходство и различия образов, являющиеся
очевидными для человека, пока ставят в тупик даже наиболее сложные
компьютерные системы распознавания. А значит, бесчисленное
количество важных приложений, в которых компьютеры могут заменить
людей в опасных, скучных или неприятных работах, по-прежнему
остаются за пределами текущих возможностей вычислительной
техники.
Компьютерное распознавание образов
пока больше напоминает искусство; научная составляющая ограничена
наличием нескольких методик, имеющих относительно небольшое
практическое применение. Инженер, конструирующий типовую систему
распознавания образов, обычно начинает с
распознавания печатного текста. Такой метод часто является
неадекватным проблеме, и старания разработчиков быстро сводятся к
разработке алгоритмов, узкоспецифичных для их личной задачи.
Обычно целью конструирования систем распознавания образов является оптимизация ее
функционирования над выборочным набором образов. Очень часто
разработчик завершает эту задачу нахождением нового, приблизительно
похожего образа, что приводит к неудачному завершению алгоритмов.
Процесс может продолжаться неопределенно долго и никогда не
приводить к устойчивому решению, достаточному для повторения
процесса восприятия реального мозга.
К счастью, мы имеем существующее доказательство, что задача может
быть решена: это система восприятия человека. Учитывая
ограниченность успехов, достигнутых в результате стремления к
механистическим изобретениям, кажется вполне логичным вернуться к
биологическим моделям и попытаться определить, каким образом они
функционируют так хорошо. Очевидно, что это трудно сделать по
нескольким причинам. Во-первых, сверхвысокая сложность человеческого
мозга затрудняет понимание принципов его устройства: нелегко понять
общие принципы функционирования и взаимодействия приблизительно 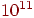 нейронов и нейронов и  синаптических связей. Кроме того, существует множество
проблем при проведении экспериментальных исследований.
Микроскопические исследования требуют тщательно подготовленных
образцов (заморозка, срезы, окраска) для получения маленького
двумерного взгляда на большую трехмерную структуру. Техника
микропроб позволяет провести анализы внутренней электрохимии узлов,
однако трудно контролировать одновременно большое количество узлов и
наблюдать их взаимодействие. Наконец, этические соображения
запрещают многие важные исследования, которые могут быть выполнены
только на живых людях. Большое значение имели эксперименты над
животными, однако животные не обладают способностями человека
описывать свои впечатления. синаптических связей. Кроме того, существует множество
проблем при проведении экспериментальных исследований.
Микроскопические исследования требуют тщательно подготовленных
образцов (заморозка, срезы, окраска) для получения маленького
двумерного взгляда на большую трехмерную структуру. Техника
микропроб позволяет провести анализы внутренней электрохимии узлов,
однако трудно контролировать одновременно большое количество узлов и
наблюдать их взаимодействие. Наконец, этические соображения
запрещают многие важные исследования, которые могут быть выполнены
только на живых людях. Большое значение имели эксперименты над
животными, однако животные не обладают способностями человека
описывать свои впечатления.
Несмотря на эти ограничения, многое было изучено благодаря
блестяще поставленным экспериментам. Например, С.Блекмор описал
опыт, когда котята выращивались в визуальном окружении, состоящем
только из горизонтальных черных и белых полос. Известно, что
определенные области коры мозга чувствительны к углу ориентации,
поэтому у этих котов не развились нейроны, распознающие вертикальные
полосы. Результат наводит на мысль, что мозг млекопитающих не
является полностью "предустановленным" даже на примитивном уровне
распознавания ориентации линий. Напротив, он постоянно
самоорганизуется, основываясь на опыте.
На микроскопическом уровне обнаружено, что нейроны обладают как
возбуждающими, так и тормозящими синапсами. Первые стремятся к
возбуждению нейрона, вторые подавляют возбуждение. Это наводит на
мысль, что мозг адаптируется либо изменением воздействия синапсов,
либо созданием или разрушением синапсов в результате воздействия
окружающей среды. Данное предположение остается пока гипотезой с
ограниченным физиологическим подтверждением. Однако исследования,
проведенные в рамках этой гипотезы, привели к созданию цифровых
моделей, некоторые из которых показывают замечательные способности к
адаптивному распознаванию образов.
Основываясь на текущих знаниях анатомии и физиологии мозга,
разработан когнитрон, гипотетическая
модель системы восприятия человека. Компьютерные модели
продемонстрировали впечатляющие способности адаптивного распознавания образов, побуждая физиологов
исследовать соответствующие механизмы мозга. Это взаимно усиливающее
взаимодействие между искусственными нейронными сетями, физиологией и
психологией может оказаться средством, которое со временем позволит
понять механизмы деятельности мозга.
Структура сети
Когнитрон состоит из иерархически
связанных слоев нейронов двух типов — тормозящих и возбуждающих.
Состояние возбуждения каждого нейрона определяется суммой его
тормозящих и возбуждающих входов. Синаптические связи идут от
нейронов одного слоя (далее слоя 1) к следующему (слою 2).
Относительно данной синаптической связи соответствующий нейрон слоя
1 является пресинаптическим, а нейрон второго слоя —
постсинаптическим. Постсинаптические нейроны связаны не со всеми
нейронами 1-го слоя, а лишь с теми, которые принадлежат их локальной
области связей. Области связей близких друг к другу
постсинаптических нейронов перекрываются, поэтому активность данного
пресинаптического нейрона будет сказываться на все более
расширяющейся области постсинаптических нейронов следующих слоев
иерархии.
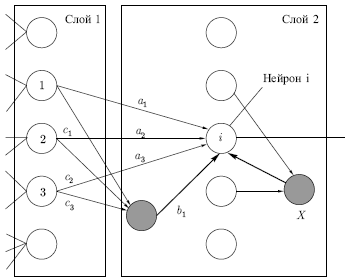
Рис. 13.1.
Вход возбуждающего постсинаптического нейрона (на рис.
13.1 — нейрон  )
определяется отношением суммы )
определяется отношением суммы  его возбуждающих входов (
его возбуждающих входов ( , ,  и и  ) к сумме ) к сумме 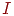 тормозящих входов (
тормозящих входов (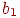 и вход от нейрона и вход от нейрона  ): ):
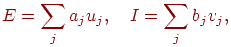
где 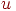 — возбуждающие входы с весами — возбуждающие входы с весами  , ,
 — тормозящие входы с весами
— тормозящие входы с весами  .
Все веса имеют положительные значения. По значениям .
Все веса имеют положительные значения. По значениям  и
и 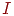 вычисляется суммарное воздействие на вычисляется суммарное воздействие на  -й нейрон: -й нейрон: 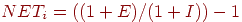 . Его
выходная активность . Его
выходная активность 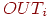 затем устанавливается равной затем устанавливается равной  , если , если  . В противном случае выход устанавливается равным нулю.
Анализ формулы для суммарного воздействия показывает, что при малом
торможении . В противном случае выход устанавливается равным нулю.
Анализ формулы для суммарного воздействия показывает, что при малом
торможении 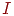 оно равно разности возбуждающего и тормозящего сигналов. В случае
же, когда оба эти сигнала велики, воздействие ограничивается
отношением. Такие особенности реакции соответствуют реакциям
биологических нейронов, способных работать в широком диапазоне
воздействий.
оно равно разности возбуждающего и тормозящего сигналов. В случае
же, когда оба эти сигнала велики, воздействие ограничивается
отношением. Такие особенности реакции соответствуют реакциям
биологических нейронов, способных работать в широком диапазоне
воздействий.
Пресинаптические тормозящие нейроны имеют ту же область связей,
что и рассматриваемый возбуждающий постсинаптический нейрон  .
Веса таких тормозящих нейронов ( .
Веса таких тормозящих нейронов ( , ,  и и  ) являются заданными и не изменяются при обучении. Их сумма
равна единице, и таким образом, выход тормозного пресинаптического
нейрона равен средней активности возбуждающих пресинаптических
нейронов в области связей: ) являются заданными и не изменяются при обучении. Их сумма
равна единице, и таким образом, выход тормозного пресинаптического
нейрона равен средней активности возбуждающих пресинаптических
нейронов в области связей:
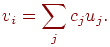
Обучение когнитрона
Так как когнитрон реализован в виде
многослойной сети, возникают сложные проблемы обучения, связанные с
выбранной структурой. Получая обучающий набор входных образов, сеть
самоорганизуется посредством изменения силы синаптических связей.
При этом отсутствуют предварительно определенные выходные образы,
представляющие требуемую реакцию сети, однако сеть самонастраивается
с целью распознавания входных образов с
замечательной точностью.
Алгоритм обучения когнитрона является
концептуально привлекательным. В заданной области слоя обучается
только наиболее сильно возбужденный нейрон. Автор сравнивает это с
"элитным обучением", при котором обучаются только "умные" элементы.
Те нейроны, которые уже хорошо обучены, что выражается силой их
возбуждения, получат приращение силы своих синапсов с целью
дальнейшего усиления своего возбуждения.
На рис.
13.2 показано, что области связи соседних узлов значительно
перекрываются. Такое расточительное дублирование функций
оправдывается взаимной конкуренцией между ближайшими узлами. Даже
если узлы в начальный момент имеют абсолютно идентичный выход,
небольшие отклонения всегда случаются; один из узлов всегда будет
иметь более сильную реакцию на входной образ, чем соседние. Его
сильное возбуждение будет оказывать сдерживающее воздействие на
возбуждение соседних узлов, и усиливаться будут только его синапсы —
синапсы соседних узлов останутся неизменными.
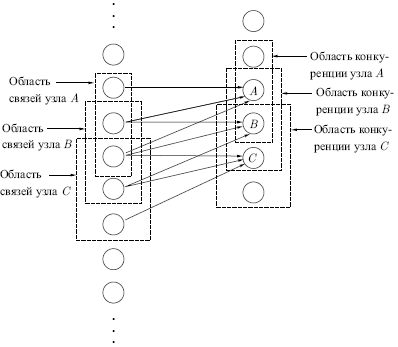
Рис. 13.2.
Возбуждающий нейрон. Можно сказать, что выход
возбуждающего нейрона в когнитроне
определяется отношением его возбуждающих входов к тормозящим входам.
Эта необычная функция имеет важные преимущества, как практические,
так и теоретические. Суммарный возбуждающий вход в нейрон является
взвешенной суммой входов от возбуждающих входов в предшествующем
слое. Аналогично суммарный вход является взвешенной суммой входов от
всех тормозящих нейронов. В символьном виде
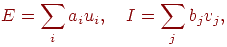
где  — вес — вес
 -го возбуждающего синапса, -го возбуждающего синапса, 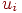 — выход — выход  -го возбуждающего нейрона, -го возбуждающего нейрона,  — вес — вес 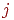 -го торозящего синапса, -го торозящего синапса,  — выход — выход 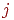 -го торозящего нейрона. -го торозящего нейрона.
Заметим, что веса имеют только положительные значения. Выход
нейрона затем вычисляется следующим образом:
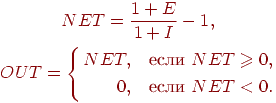
Предполагая, что NET имеет положительное значение, можно
записать:
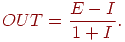
Когда тормозящий вход мал ( ), OUT может быть аппроксимировано как ), OUT может быть аппроксимировано как 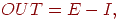
что соответствует выражению для обычного линейного порогового
элемента (с нулевым порогом).
Алгоритм обучения когнитрона позволяет
весам синапсов возрастать без ограничений. Благодаря отсутствию
механизма уменьшения, веса просто возрастают в процессе обучения. В
обычных линейных пороговых элементах это привело бы к произвольно
большому выходу элемента. В когнитроне
большие возбуждающие и тормозящие входы дают в результате выход,
который вычисляется по ограничивающей формуле вида
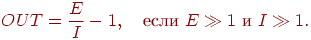
В данном случае OUT определяется отношением возбуждающих входов к
тормозящим входам, а не их разностью. Следовательно, величина OUT
ограничивается, если оба входа возрастают в одном и том же диапазоне
 .
Тогда .
Тогда  и и 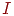 можно выразить следующим образом:
можно выразить следующим образом: 
и после некоторых преобразований
![OUT = \frac{p-q}{2q}\cdot\left[1+\th\left(\frac{\log(pq)}{2}\right)\right].](a0503cfb4d22a124354137b459e7e54d.png)
Эта функция возрастает по закону Вебера—Фехнера, который часто
применяется в нейрофизиологии для аппроксимации нелинейных
соотношений входа/выхода сенсорных нейронов. При использовании этого
соотношения нейрон когнитрона в точности
эмулирует реакцию биологических нейронов — и становится как мощным
вычислительным элементом, так и точной моделью физиологического
моделирования.
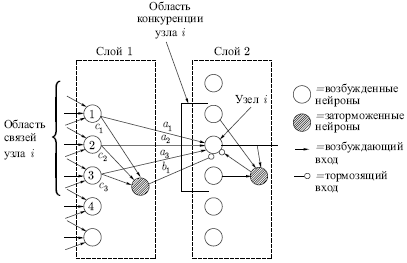
Рис. 13.3.
Тормозящие нейроны. В когнитроне слой состоит из возбуждающих и
тормозящих узлов. Как показано на рис.
13.3, нейрону слоя 2 присуща область связи, для которой он имеет
синаптические соединения с набором выходов нейронов в слое 1.
Аналогично, в слое 1 существует тормозящий нейрон, имеющий ту же
область связи. Синаптические веса тормозящих узлов не изменяются в
процессе обучения; их веса заранее установлены таким образом, что
сумма весов в любом из тормозящих нейронов равна единице. В
соответствии с этими ограничениями, выход тормозящего узла INHIB
является взвешенной суммой его входов, которые в данном случае
представляют собой среднее арифметическое выходов возбуждающих
нейронов, к которым подсоединен данный выход. Таким образом,
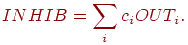
где 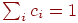 , ,  — возбуждающий вес — возбуждающий вес  . .
Процедура обучения. Как объяснялось ранее, веса
возбуждающих нейронов изменяются только тогда, когда нейрон
возбужден сильнее, чем любой из узлов в области конкуренции. Если
это так, изменение в процессе обучения любого из его весов может
быть определено следующим образом: 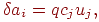
где  —
тормозящий вес связи нейрона —
тормозящий вес связи нейрона 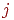 в слое 1 с тормозящим нейроном
в слое 1 с тормозящим нейроном  , ,
 — выход нейрона — выход нейрона 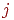 в слое 1,
в слое 1,  —
возбуждающий вес —
возбуждающий вес  , ,
 — нормирующий коэффициент обучения.
— нормирующий коэффициент обучения.
Изменение тормозящих весов нейрона  в слое 2 пропорционально отношению взвешенной суммы возбуждающих
входов к удвоенному тормозящему входу. Вычисления проводятся по
формуле
в слое 2 пропорционально отношению взвешенной суммы возбуждающих
входов к удвоенному тормозящему входу. Вычисления проводятся по
формуле
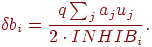
Когда возбужденных нейронов в области конкуренции нет, для
изменения весов используются другие выражения. Это необходимо,
поскольку процесс обучения начинается с нулевыми значениями весов;
поэтому первоначально нет возбужденных нейронов ни в одной области
конкуренции, и обучение производиться не может. Во всех случаях,
когда победителя в области конкуренции нейронов нет, изменение весов
нейронов вычисляется следующим образом: 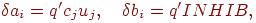
где  —
положительный обучающий коэффициент, меньший, чем —
положительный обучающий коэффициент, меньший, чем  . .
Приведенная стратегия настройки гарантирует, что узлы с большой
реакцией заставляют возбуждающие синапсы, которыми они управляют,
увеличиваться сильнее, чем тормозящие синапсы. Верна и обратная
зависимость: узлы, имеющие малую реакцию, вызывают малое возрастание
возбуждающих синапсов, но большее возрастание тормозящих синапсов.
Таким образом, если узел 1 в слое 1 имеет больший выход, синапс  возрастет больше, чем синапс возрастет больше, чем синапс 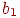 . И наоборот, узлы, имеющие малый выход, обеспечат малую
величину для приращения . И наоборот, узлы, имеющие малый выход, обеспечат малую
величину для приращения  . Однако другие узлы в области связи будут возбуждаться,
тем самым увеличивая сигнал INHIB и значения . Однако другие узлы в области связи будут возбуждаться,
тем самым увеличивая сигнал INHIB и значения 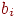 . .
В процессе обучения веса каждого узла в слое 2 настраиваются
таким образом, что вместе они составляют шаблон, соответствующий
образам, которые часто предъявляются в процессе обучения. При
предъявлении сходного образа шаблон соответствует ему и узел
вырабатывает большой выходной сигнал. Сильно отличающийся образ
вызывает малый выход и обычно подавляется конкуренцией.
Латеральное торможение. На рис.
13.3 показано, что каждый нейрон слоя 2 получает латеральное
торможение от нейронов, расположенных в его области конкуренции.
Тормозящий нейрон суммирует входы от всех нейронов в области
конкуренции и вырабатывает сигнал, стремящийся к торможению целевого
нейрона. Этот метод является эффектным, но с вычислительной точки
зрения медленным. Он охватывает большую систему с обратной связью,
включающую каждый нейрон в слое; для его стабилизации может
потребоваться большое количество вычислительных итераций.
Для ускорения вычислений используется остроумный метод
ускоренного латерального торможения (см. рис.
13.4). Здесь дополнительный узел латерального торможения
обрабатывает выход каждого возбуждающего узла для моделирования
требуемого латерального торможения. Сначала он определяет сигнал,
равный суммарному тормозящему влиянию в области конкуренции:
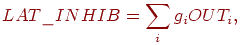
где 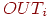 —
выход —
выход  -го нейрона в области конкуренции, -го нейрона в области конкуренции,  — вес связи от этого нейрона к латерально-тормозящему
нейрону; — вес связи от этого нейрона к латерально-тормозящему
нейрону;  выбраны таким образом, что
выбраны таким образом, что 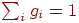 . .
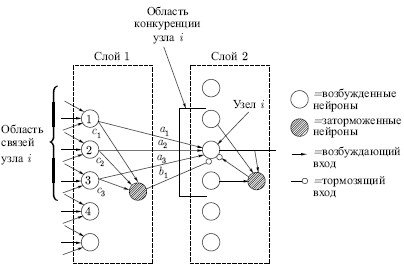
Рис. 13.4.
Выход тормозящего нейрона  затем вычисляется следующим образом: затем вычисляется следующим образом:
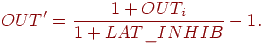
Благодаря тому что все вычисления, связанные с таким типом
латерального торможения, являются нерекурсивными, они могут быть
проведены за один проход для слоя. Такой подход позволяет весьма
эффективно экономить вычисления.
Метод ускоренного латерального торможения решает и другую сложную
проблему. Предположим, что узел в слое 2 возбуждается сильно, но
возбуждение соседних узлов уменьшается постепенно с увеличением
расстояния. При использовании обычного латерального торможения будет
обучаться только центральный узел: другие узлы определят, что
центральный узел в их области конкуренции имеет более высокий выход.
С предлагаемой системой латерального торможения такой ситуации
случиться не может. Множество узлов может обучаться одновременно, и
процесс обучения становится более достоверным.
Когнитрон как модель зрительной коры мозга
Анализ, проводимый до этого момента, был упрощен рассмотрением
только одномерных слоев. В действительности когнитрон конструировался как каскад двумерных
слоев, причем в любом слое каждый нейрон получает входы от набора
нейронов на части двумерного плана, составляющей его область связи в
предыдущем слое.
С этой точки зрения когнитрон
организован подобно зрительной коре человеческого мозга, которая
представляет собой трехмерную структуру, состоящую из нескольких
различных слоев. Оказывается, что каждый слой коры головного мозга
реализует различные уровни обобщения; входной слой чувствителен к
простым образам, таким как линии и их ориентации в определенных
областях "поля зрения", в то время как реакция других слоев является
более сложной, абстрактной и независимой от позиции образа.
Аналогичные функции реализованы в когнитроне путем моделирования организации
зрительной коры. На рис.
13.5 показано, что нейроны когнитрона
в слое 2 реагируют на определенную небольшую область входного слоя
1. Нейрон в слое 3 связан с набором нейронов слоя 2, тем самым
реагируя косвенно на более широкий набор нейронов слоя 1. Далее,
нейроны в последующих слоях чувствительны к более широким областям
входного образа до тех пор, пока в выходном слое каждый нейрон не
станет реагировать на все входное поле.
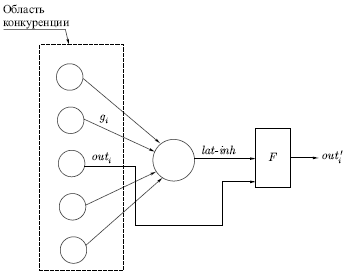
Рис. 13.5.
Если область связи нейронов имеет постоянный размер во всех
слоях, требуется большое количество слоев для перекрытия всего
входного поля выходными нейронами. Количество слоев может быть
уменьшено, если расширить область связи в последующих слоях. К
сожалению, в результате может произойти настолько большое перекрытие
областей связи, что нейроны выходного слоя будут иметь одинаковую
реакцию. Для решения этой проблемы может быть использовано
расширение области конкуренции. Так как в данной области конкуренции
может возбудиться только один узел, влияние малой разницы в реакциях
нейронов выходного слоя усиливается.
В альтернативном варианте связи с предыдущим слоем могут быть
распределены вероятностно с большинством синаптических связей в
ограниченной области и с более длинными соединениями, встречающимися
намного реже. Здесь смоделировано вероятностное распределение
нейронов, обнаруженное в мозге. В когнитроне это позволяет каждому нейрону
выходного слоя реагировать на полное входное поле при наличии
ограниченного количества слоев.
Результаты моделирования
В качестве примера рассмотрим компьютерное моделирование
четырехслойного когнитрона,
предназначенного для целей распознавания
образов. Каждый слой состоит из массива  возбуждающих нейронов и такого же количества тормозящих нейронов.
Область связи представляет собой квадрат, включающий
возбуждающих нейронов и такого же количества тормозящих нейронов.
Область связи представляет собой квадрат, включающий  нейронов. Область конкуренции имеет форму ромба высотой и
шириной в 5 нейронов. Латеральное торможение охватывает область нейронов. Область конкуренции имеет форму ромба высотой и
шириной в 5 нейронов. Латеральное торможение охватывает область  нейронов. Нормирующие параметры обучения установлены таким
образом, что нейронов. Нормирующие параметры обучения установлены таким
образом, что 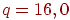 и и  . Веса синапсов проинициализированы в 0. . Веса синапсов проинициализированы в 0.
Сеть обучалась путем предъявления на входном слое пяти
стимулирующих образов, представляющих собой изображения арабских
цифр от 0 до 4. Веса сети настраивались после предъявления каждой
цифры, входной набор подавался на вход сети циклически до тех пор,
пока каждый образ не был предъявлен суммарно 20 раз.
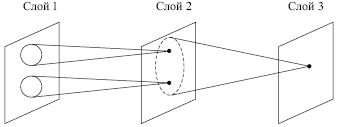
Рис. 13.6.
Эффективность процесса обучения оценивалась путем запуска сети в
реверсивном режиме; выходные образы, являющиеся реакцией сети,
подавались на выходные нейроны и распространялись обратно к входному
слою. Образы, полученные во входном слое, затем сравнивались с
исходным входным образом. Чтобы сделать это, обычные
однонаправленные связи принимались проводящими в обратном
направлении и латеральное торможение отключалось. На рис.
13.6 приведены типичные результаты тестирования. В столбце 2
показаны образы, произведенные каждой цифрой на выходе сети; они
возвращались обратно, вырабатывая на входе сети образ, близкий к
точной копии исходного входного образа. Для столбца 4 на выход сети
подавался только выход нейрона, имеющего максимальное возбуждение.
Результирующие образы в точности те же, что и в случае подачи
полного выходного образа, за исключением цифры 0, для которой узел с
максимальным выходом располагался на периферии и не покрывал
полностью входного поля.
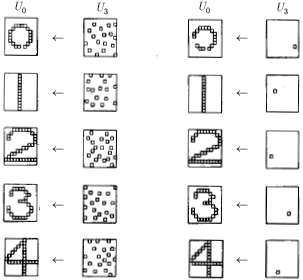
Рис. 13.7.
|




