|
Искусственные нейронные сети обучаются самыми разнообразными
методами. К счастью, большинство методов обучения исходят из общих
предпосылок и имеют много идентичных характеристик. Целью данного
приложения является обзор некоторых фундаментальных алгоритмов с
точки зрения их текущей применимости и исторической важности. После
ознакомления с этими фундаментальными алгоритмами другие основанные
на них алгоритмы будут достаточно легки для понимания, и новые
разработки также могут быть лучше поняты и развиты.
Обучение с учителем и без учителя
Обучающие алгоритмы могут быть классифицированы как алгоритмы
обучения с учителем и обучения без учителя. В первом случае
существует учитель, который предъявляет
входные образы сети, сравнивает результирующие выходы с требуемыми,
а затем настраивает веса сети таким образом, чтобы уменьшить
различия. Трудно представить такой обучающий механизм в
биологических системах; следовательно, хотя данный подход привел к
большим успехам при решении прикладных задач, он отвергается теми
исследователями, кто полагает, что искусственные нейронные сети
обязательно должны использовать те же механизмы, что и человеческий
мозг.
Во втором случае обучение проводится без
учителя: при предъявлении входных образов сеть
самоорганизуется, настраивая свои веса согласно определенному
алгоритму. Требуемый выход в процессе обучения не указан, поэтому
результаты определения возбуждающих образов для конкретных нейронов
непредсказуемы. При этом, однако, сеть организуется в форме,
отражающей существенные характеристики обучающего набора. Например,
входные образы могут быть классифицированы согласно степени их
сходства так, что образы одного класса активизируют один и тот же
выходной нейрон.
Метод обучения Хэбба
Работы Д.О. Хэбба обеспечили основу для большинства алгоритмов
обучения, которые были разработаны позже. Хэбб определял, что
обучение в биологических системах происходит посредством некоторых
физических изменений в нейронах, однако не определил, как это
осуществляется в действительности. Основываясь на физиологических и
психологических исследованиях, Хэбб интуитивно выдвинул гипотезу о
том, каким образом может обучаться набор биологических нейронов. Его
теория предполагает только локальное взаимодействие между нейронами
при отсутствии глобального учителя;
следовательно, обучение является неуправляемым. Несмотря на то, что
его работа не включает математического анализа, идеи, изложенные в
ней, настолько ясны и изящны, что получили статус универсальных
допущений. Его книга стала классической и широко изучается
специалистами, которых серьезно интересует эта область.
Алгоритм обучения Хэбба
По существу, Хэбб предположил, что синаптическое соединение двух
нейронов усиливается, если оба эти нейрона возбуждены. Это можно
представить как усиление синапса в соответствии с корреляцией
уровней возбужденных нейронов, соединяемых данным синапсом. Поэтому
алгоритм обучения Хэбба иногда называется корреляционным
алгоритмом.
Идея алгоритма выражается следующим равенством: 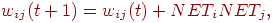
где 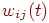 — сила
синапса от нейрона — сила
синапса от нейрона  к нейрону
к нейрону 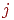 в момент времени в момент времени 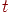 ; ;
 — уровень возбуждения пресинаптического нейрона; — уровень возбуждения пресинаптического нейрона; 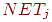 — уровень возбуждения постсинаптического нейрона. — уровень возбуждения постсинаптического нейрона.
Концепция Хэбба отвечает на сложный вопрос: каким образом
обучение может проводиться без учителя? В
методе Хэбба обучение является исключительно локальным явлением,
охватывающим только два нейрона и соединяющий их синапс; не
требуется глобальной системы обратной связи для развития нейронных
образований.
Последующее использование метода Хэбба для обучения нейронных
сетей привело к большим успехам, но наряду с этим показало
ограниченность метода; некоторые образы просто не могут
использоваться для обучения этим методом. В результате появилось
большое количество расширений и нововведений, большинство из которых
в значительной степени основано на работе Хэбба.
Метод сигнального обучения Хэбба
Как мы видели, выход NET простого искусственного нейрона является
взвешенной суммой его входов. Это может быть выражено следующим
образом:
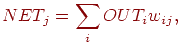
где 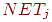 —
выход NET нейрона —
выход NET нейрона 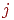 , ,
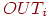 — выход нейрона — выход нейрона  , ,
 — вес связи нейрона — вес связи нейрона  с нейроном
с нейроном 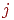 . .
Можно показать, что в этом случае линейная многослойная сеть не
является более мощной, чем однослойная сеть; рассматриваемые
возможности сети могут быть улучшены только введением нелинейности в
передаточную функцию нейрона. Говорят, что сеть, использующая
сигмоидальную функцию активации и метод обучения Хэбба, обучается по
сигнальному методу Хэбба. В этом случае уравнение Хэбба
модифицируется следующим образом:
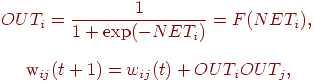
где 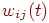 — сила
синапса от нейрона — сила
синапса от нейрона  к нейрону
к нейрону 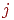 в момент времени в момент времени 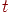 , ,
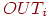 — выходной уровень пресинаптического нейрона равный — выходной уровень пресинаптического нейрона равный 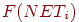 , ,  — выходной уровень постсинаптического нейрона, равный — выходной уровень постсинаптического нейрона, равный 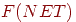 . .
Метод дифференциального обучения Хэбба
Метод сигнального обучения Хэбба предполагает вычисление свертки
предыдущих изменений выходов для определения изменения весов. Данный
же метод, называемый методом дифференциального обучения Хэбба,
использует следующее равенство: ![w_{ij}(t+1)=w_{ij}(t)+[OUT_i(t)-OUT_i(t-1)][OUT_j(t)-OUT_j(t-1)],](2adec2033a009bf63f6845671c9cfbf8.png)
где 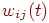 — сила
синапса от нейрона — сила
синапса от нейрона  к нейрону
к нейрону 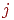 в момент времени в момент времени 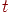 , ,
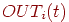 — выходной уровень пресинаптического нейрона в момент
времени — выходной уровень пресинаптического нейрона в момент
времени 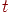 , , 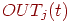 — выходной уровень постсинаптического нейрона в момент
времени — выходной уровень постсинаптического нейрона в момент
времени 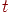 . .
Входные и выходные звезды
Много общих идей, используемых в искусственных нейронных сетях,
прослеживаются в работах С. Гроссберга; в качестве примера можно
указать конфигурации входных и выходных звезд, используемые во
многих сетевых парадигмах. Входная звезда, как показано на рис.
15.1, состоит из нейрона, на который подается группа входов
через синапсические веса. Выходная звезда, показанная на рис.
15.2, является нейроном, управляющим группой весов. Входные и
выходные звезды могут быть взаимно соединены в сети любой сложности;
Гроссберг рассматривает их как модель определенных биологических
функций. Вид звезды определяет ее название, однако, звезды обычно
изображаются в сети несколько иначе.
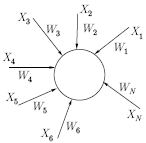
Рис. 15.1.
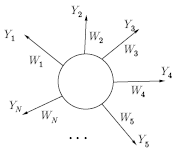
Рис. 15.2.
Обучение входной звезды
Входная звезда выполняет распознавание образов, т. е. она
обучается реагировать на определенный входной вектор  и ни на какой другой. Это обучение реализуется, настраивая
веса таким образом, чтобы они соответствовали входному вектору.
Выход входной звезды определяется как взвешенная сумма ее входов,
это описано в предыдущих разделах. С другой точки зрения, выход
можно рассматривать как свертку входного вектора с весовым вектором
или меру сходства нормализованных векторов. Следовательно, нейрон
должен реагировать наиболее сильно на входной образ, которому был
обучен. и ни на какой другой. Это обучение реализуется, настраивая
веса таким образом, чтобы они соответствовали входному вектору.
Выход входной звезды определяется как взвешенная сумма ее входов,
это описано в предыдущих разделах. С другой точки зрения, выход
можно рассматривать как свертку входного вектора с весовым вектором
или меру сходства нормализованных векторов. Следовательно, нейрон
должен реагировать наиболее сильно на входной образ, которому был
обучен.
Процесс обучения выражается следующим образом: ![w_i(t+1)=w_i(t)+\alpha[x_i-w_i(t)],](3ca5705eb9dcc876f9284e5b14342978.png)
где  — вес
входа — вес
входа 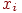 , , 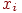 — —  -й вход, -й вход,  — нормирующий коэффициент обучения, который имеет
начальное значение 0,1 и постепенно уменьшается в процессе
обучения. — нормирующий коэффициент обучения, который имеет
начальное значение 0,1 и постепенно уменьшается в процессе
обучения.
После завершения обучения предъявление входного вектора Х будет
активизировать обученный входной нейрон. Это можно рассматривать как
единый обучающий цикл, если  установлен в 1, однако в этом случае исключается
способность входной звезды к обобщению. Хорошо обученная входная
звезда будет реагировать не только на определенный единичный вектор,
но также и на незначительные изменения этого вектора. Это
достигается постепенной настройкой нейронных весов при предъявлении
в процессе обучения векторов, представляющих нормальные вариации
входного вектора. Веса настраиваются таким образом, чтобы усреднить
величины обучающих векторов, и нейроны получают способность
реагировать на любой вектор этого класса. установлен в 1, однако в этом случае исключается
способность входной звезды к обобщению. Хорошо обученная входная
звезда будет реагировать не только на определенный единичный вектор,
но также и на незначительные изменения этого вектора. Это
достигается постепенной настройкой нейронных весов при предъявлении
в процессе обучения векторов, представляющих нормальные вариации
входного вектора. Веса настраиваются таким образом, чтобы усреднить
величины обучающих векторов, и нейроны получают способность
реагировать на любой вектор этого класса.
Обучение выходной звезды
В то время как входная звезда возбуждается всякий раз при
появлении определенного входного вектора, выходная звезда имеет
дополнительную функцию: она вырабатывает требуемый возбуждающий
сигнал для других нейронов всякий раз, когда возбуждается.
Для того чтобы обучить нейрон выходной звезды, его веса
настраиваются в соответствии с требуемым целевым вектором. Алгоритм
обучения может быть представлен символически следующим
образом: ![w_i(t+1)=w_i(t)+\beta[y_i-w_i(t)],](ef2d9bcd49f9ff5702b4c95ce7296663.png)
где 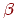 представляет собой нормирующий коэффициент обучения, который вначале
приблизительно равен единице и постепенно уменьшается до нуля в
процессе обучения.
представляет собой нормирующий коэффициент обучения, который вначале
приблизительно равен единице и постепенно уменьшается до нуля в
процессе обучения.
Как и для входной звезды, веса выходной звезды постепенно
настраиваются над множеством векторов, представляющих собой обычные
вариации идеального вектора. В этом случае выходной сигнал нейронов
является статистической характеристикой обучающего набора и может в
действительности сходиться в процессе обучения к идеальному вектору
при предъявлении только искаженных версий вектора.
Обучение персептрона
В 1957 г. Р.Розенблатт разработал модель, которая вызвала большой
интерес у исследователей. Несмотря на некоторые ограничения ее
исходной формы, она стала основой для многих современных, наиболее
сложных алгоритмов обучения с
учителем.
Персептрон является двухуровневой нерекуррентной сетью, вид
которой показан на рис.
15.3. Она использует алгоритм обучения с
учителем; другими словами, обучающая выборка состоит из
множества входных векторов, для каждого из которых указан свой
требуемый вектор цели. Компоненты входного вектора представлены
непрерывным диапазоном значений; компоненты вектора цели являются
двоичными величинами (0 или 1). После обучения сеть получает на
входе набор непрерывных входов и вырабатывает требуемый выход в виде
вектора с бинарными компонентами.
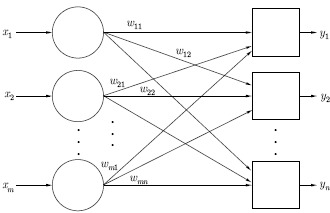
Рис. 15.3.
Обучение осуществляется следующим образом:
- Рандомизируются все веса сети в малые величины.
-
На вход сети подается входной обучающий вектор  и вычисляется сигнал NET от каждого нейрона, используя
стандартное выражение и вычисляется сигнал NET от каждого нейрона, используя
стандартное выражение
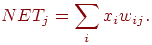
-
Вычисляется значение пороговой функции активации для сигнала
NET от каждого нейрона следующим образом:
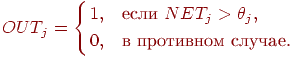
Здесь 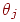 представляет собой порог, соответствующий нейрону представляет собой порог, соответствующий нейрону 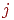 (в простейшем случае все нейроны имеют один и тот же
порог). (в простейшем случае все нейроны имеют один и тот же
порог).
-
Вычисляется ошибка для каждого нейрона посредством вычитания
полученного выхода из требуемого выхода:
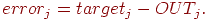
-
Каждый вес модифицируется следующим образом:
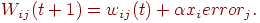
- Повторяются шаги со второго по пятый до тех пор, пока ошибка
не станет достаточно малой.
Метод обучения Уидроу—Хоффа
Как мы видели, персептрон ограничивается бинарными выходами.
Б.Уидроу вместе со студентом университета М.Хоффом расширили
алгоритм обучения персептрона для случая непрерывных выходов,
используя сигмоидальную функцию. Второй их впечатляющий результат —
разработка математического доказательства, что сеть при определенных
условиях будет сходиться к любой функции, которую она может
представить. Их первая модель — Адалин — имеет один выходной нейрон,
более поздняя модель — Мадалин — расширяет ее для случая с многими
выходными нейронами.
Выражения, описывающие процесс обучения Адалина, очень схожи с
персептронными. Существенные отличия имеются в четвертом шаге, где
используются непрерывные сигналы NET вместо бинарных OUT.
Модифицированный шаг 4 в этом случае реализуется следующим
образом:
4. Вычисляется ошибка для каждого нейрона посредством вычитания
полученного выхода из требуемого выхода: 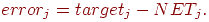
Метод статистического обучения
Однослойные сети несколько ограниченны с точки зрения задач,
которые они могут решать; однако, в течение многих лет отсутствовали
методы обучения многослойных сетей. Статистическое обучение является
как раз таким методом и обеспечивает путь решения этих проблем.
По аналогии, обучение сети статистическими способами подобно
процессу отжига металла. В процессе отжига температура металла
вначале повышается, пока атомы не начнут перемещаться почти
свободно. Затем температура постепенно уменьшается и атомы
непрерывно стремятся к минимальной энергетической конфигурации. При
некоторой низкой температуре атомы переходят на низший
энергетический уровень.
В искусственных нейронных сетях полная величина энергии сети
определяется как функция определенного множества сетевых переменных.
Искусственная переменная температуры инициируется в большую
величину, тем самым позволяя сетевым переменным претерпевать большие
случайные изменения. Изменения, приводящие к уменьшению полной
энергии сети, сохраняются; изменения, приводящие к увеличению
энергии, сохраняются в соответствии с вероятностной функцией.
Искусственная температура постепенно уменьшается с течением времени,
и сеть конвергирует в состояние минимума полной энергии.
Существует много вариаций на тему статистического обучения.
Например, глобальная энергия может быть определена как средняя
квадратичная ошибка между полученным и желаемым выходным вектором из
обучаемого множества, а переменными могут быть веса сети. В этом
случае сеть может быть обучена, начиная с высокой искусственной
температуры, путем выполнения следующих шагов:
- Подать обучающий вектор на вход сети и вычислить выход
согласно соответствующим сетевым правилам.
- Вычислить значение средней квадратичной ошибки между желаемым
и полученным выходными векторами.
- Изменить сетевые веса случайным образом, затем вычислить новый
выход и результирующую ошибку. Если ошибка уменьшилась, оставить
измененный вес; если ошибка увеличилась, оставить измененный вес с
вероятностью, определяемой распределением Больцмана. Если
изменения весов не производится, то вернуть вес к его предыдущему
значению.
- Повторить шаги с 1 по 3, постепенно уменьшая искусственную
температуру.
Если величина случайного изменения весов определяется в
соответствии с распределением Больцмана, сходимость к глобальному
минимуму будет осуществляться только в том случае, когда температура
изменяется обратно пропорционально логарифму прошедшего времени
обучения. Это может привести к невероятной длительности процесса
обучения, поэтому большое внимание уделялось поиску более быстрых
методов. Выбором размера шага в соответствии с распределением Коши
может быть достигнуто уменьшение температуры, обратно
пропорциональное обучающему времени, что существенно уменьшает
время, требуемое для сходимости.
Заметим, что существует класс статистических методов для
нейронных сетей, в которых переменными сети являются выходы
нейронов, а не веса.
Самоорганизация
Самоорганизующихся структуры классифицируют образы,
представленные векторными величинами, в которых каждая компонента
вектора соответствует элементу образа. Алгоритмы Кохонена
основываются на технике обучения без
учителя. После обучения подача входного вектора из данного
класса будет приводить к выработке возбуждающего уровня в каждом
выходном нейроне; нейрон с максимальным возбуждением представляет
классификацию. Так как обучение проводится без указания целевого
вектора, то нет возможности определять заранее, какой нейрон будет
соответствовать данному классу входных векторов. Тем не менее, это
планирование легко проводится путем тестирования сети после
обучения.
Алгоритм трактует набор из  входных весов нейрона как вектор в
входных весов нейрона как вектор в  -мерном пространстве. Перед обучением каждый компонент
этого вектора весов инициализируется в случайную величину. Затем
каждый вектор нормализуется в вектор с единичной длиной в
пространстве весов - для этого выполняется деление каждого
случайного веса на квадратный корень из суммы квадратов компонент
этого весового вектора. -мерном пространстве. Перед обучением каждый компонент
этого вектора весов инициализируется в случайную величину. Затем
каждый вектор нормализуется в вектор с единичной длиной в
пространстве весов - для этого выполняется деление каждого
случайного веса на квадратный корень из суммы квадратов компонент
этого весового вектора.
Все входные векторы обучающего набора также нормализуются и сеть
обучается согласно следующему алгоритму:
- Вектор
 подается на вход сети. подается на вход сети.
-
Определяются расстояния 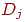 (в (в  -мерном пространстве) между -мерном пространстве) между  и весовыми векторами и весовыми векторами 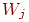 каждого нейрона. В евклидовом пространстве это
расстояние вычисляется по следующей формуле: каждого нейрона. В евклидовом пространстве это
расстояние вычисляется по следующей формуле:
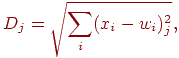
где 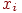 —
компонента —
компонента  входного вектора входного вектора  , ,  — вес входа — вес входа  нейрона нейрона 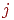 . .
- Нейрон, который имеет весовой вектор, самый близкий к
 , объявляется победителем. Этот вектор, называемый , объявляется победителем. Этот вектор, называемый 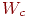 , становится основным в группе весовых векторов, которые
лежат в пределах расстояния , становится основным в группе весовых векторов, которые
лежат в пределах расстояния  от от 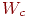 . .
-
Группа весовых векторов настраивается в соответствии со
следующим выражением: ![W_j(t+1)=W_j(t)+\alpha[X-W_j(t)]](a6393b2afbe40a24d0ec4cf350803101.png)
для всех весовых векторов в пределах расстояния  от от 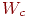 . .
- Повторяются шаги с 1 по 4 для каждого входного
вектора.
В процессе обучения нейронной сети значения  и
и  постепенно уменьшаются. Рекомендуется, чтобы коэффициент
постепенно уменьшаются. Рекомендуется, чтобы коэффициент  в начале обучения устанавливался приблизительно равным
единице и уменьшался в процессе обучения до нуля, в то время как в начале обучения устанавливался приблизительно равным
единице и уменьшался в процессе обучения до нуля, в то время как
 может в начале обучения равняться максимальному расстоянию между
весовыми векторами и в конце обучения стать настолько маленьким, что
будет обучаться только один нейрон.
может в начале обучения равняться максимальному расстоянию между
весовыми векторами и в конце обучения стать настолько маленьким, что
будет обучаться только один нейрон.
В соответствии с существующей точкой зрения, точность
классификации будет улучшаться при дополнительном обучении. Согласно
рекомендации Кохонена, для получения хорошей статистической точности
количество обучающих циклов должно быть, по крайней мере, в 500 раз
больше количества выходных нейронов.
Обучающий алгоритм настраивает весовые векторы в окрестности
возбужденного нейрона таким образом, чтобы они были более схожими с
входным вектором. Так как все векторы нормализуются в векторы с
единичной длиной, они могут рассматриваться как точки на поверхности
единичной гиперсферы. В процессе обучения группа соседних весовых
точек перемещается ближе к точке входного вектора. Предполагается,
что входные векторы фактически группируются в классы в соответствии
с их положением в векторном пространстве. Определенный класс будет
ассоциироваться с определенным нейроном, перемещая его весовой
вектор в направлении центра класса и способствуя его возбуждению при
появлении на входе любого вектора данного класса.
После обучения классификация выполняется в два шага: подачей на
вход сети испытуемого вектора и вычисления возбуждения для каждого
нейрона, с последующим выбором нейрона с наивысшим возбуждением как
индикатора правильной классификации.
|




