Персептроны и зарождение искусственных нейронных сетей
В качестве предмета исследования искусственные нейронные сети
впервые заявили о себе в 1940-е годы. Стремясь воспроизвести функции
человеческого мозга, исследователи создали простые аппаратные (а
позже программные) модели биологического нейрона и системы его
соединений. Когда нейрофизиологи достигли более глубокого понимания
нервной системы человека, эти ранние попытки стали восприниматься
как весьма грубые аппроксимации. Тем не менее, на этом пути были
достигнуты впечатляющие результаты, стимулировавшие дальнейшие
исследования, которые привели к созданию более изощренных сетей.
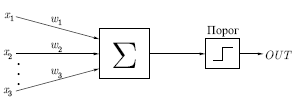
Рис. 2.1.
Первое систематическое изучение искусственных нейронных сетей
было предпринято Маккалокком и Питтсом в 1943 г. Позднее они
исследовали сетевые парадигмы для распознавания изображений,
подвергаемых сдвигам и поворотам. Простая нейронная модель,
показанная на рис.
2.1, использовалась в большей части их работ. Элемент 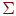 умножает каждый вход умножает каждый вход  на вес на вес  и суммирует взвешенные входы. Если полученная сумма больше
заданного порогового значения, выход равен единице, в противном
случае — нулю. Эти системы (и множество им подобных) получили
название персептронов. Они состоят из
одного слоя искусственных нейронов, соединенных с помощью весовых
коэффициентов с множеством входов (см. рис.
2.2), хотя, в принципе, описываются и более сложные системы. В
60-е годы персептроны вызвали большой
интерес и оптимизм. Одной из первых искусственных сетей, способных к
перцепции (восприятию) и формированию реакции на воспринятый
раздражитель, явился PERCEPTRON Розенблатта (F.Rosenblatt, 1957).
Персептрон рассматривался его автором не
как конкретное техническое (вычислительное) устройство, а как модель
работы мозга. Розенблатт называл такую нейронную сеть трехслойной,
однако, по современной терминологии, представленная сеть обычно
называется однослойной, так как имеет только один слой
нейропроцессорных элементов. и суммирует взвешенные входы. Если полученная сумма больше
заданного порогового значения, выход равен единице, в противном
случае — нулю. Эти системы (и множество им подобных) получили
название персептронов. Они состоят из
одного слоя искусственных нейронов, соединенных с помощью весовых
коэффициентов с множеством входов (см. рис.
2.2), хотя, в принципе, описываются и более сложные системы. В
60-е годы персептроны вызвали большой
интерес и оптимизм. Одной из первых искусственных сетей, способных к
перцепции (восприятию) и формированию реакции на воспринятый
раздражитель, явился PERCEPTRON Розенблатта (F.Rosenblatt, 1957).
Персептрон рассматривался его автором не
как конкретное техническое (вычислительное) устройство, а как модель
работы мозга. Розенблатт называл такую нейронную сеть трехслойной,
однако, по современной терминологии, представленная сеть обычно
называется однослойной, так как имеет только один слой
нейропроцессорных элементов.
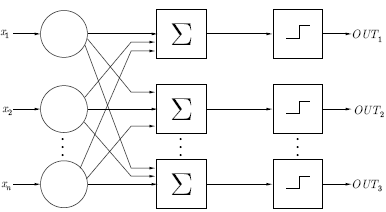
Рис. 2.2.
В Корнеллской авиационной лаборатории была разработана
электротехническая модель персептрона
MARK-1, которая содержала 8 выходных элементов. На этом персептроне была проведена серия экспериментов
по распознаванию букв алфавита и геометрических образов.
Ф. Розенблатт доказал замечательную теорему об обучении персептронов (которую мы рассмотрим на
следующей лекции). Д. Уидроу дал ряд убедительных демонстраций
систем персептронного типа, и исследователи во всем мире
стремились изучить возможности этих систем. Первоначальная эйфория
сменилась разочарованием, когда оказалось, что персептроны не способны обучаться решению ряда
простых задач. Минский строго проанализировал эту проблему и
показал, что имеются жесткие ограничения того, что могут выполнять
однослойные персептроны, и,
следовательно, того, чему они могут обучаться. Так как в то время
методы обучения многослойных сетей не были известны, исследователи
занялись более многообещающими проектами, и исследования в области
нейронных сетей пришли в упадок. Недавнее открытие методов обучения
многослойных сетей привело к возрождению интереса и возобновлению
исследований.
Работа М.Л.Минского, возможно, и охладила пыл энтузиастов персептрона, но обеспечила время для
необходимой консолидации и развития лежащей в основе теории. Важно
отметить, что анализ Минского не был опровергнут. Он остается
актуальным исследованием и должен непременно учитываться как часть
базовых знаний, чтобы ошибки 60-х годов не повторились. Несмотря на
свои ограничения, персептроны широко
изучались. Теория персептронов является
основой для многих других типов искусственных нейронных сетей, персептроны иллюстрируют важные принципы. В
силу этих причин они являются логической исходной точкой для
изучения искусственных нейронных сетей.
Персептронная представляемость
Доказательство теоремы обучения персептрона показало, что персептрон способен научиться всему, что он
способен представлять. Важно при этом уметь различать
представляемость и обучаемость. Понятие представляемости относится к
способности персептрона (или другой сети)
моделировать определенную функцию. Обучаемость же требует наличия
систематической процедуры настройки весов сети для реализации этой
функции.
Для иллюстрации проблемы представляемости допустим, что у нас
есть множество карт, помеченных цифрами от 0 до 9. Допустим также,
что мы обладаем гипотетической машиной, способной отличать карты с
нечетным номером от карт с четным номером и зажигающей индикатор на
своей панели при предъявлении карты с нечетным номером. Представима
ли такая машина персептроном? То есть
возможно ли сконструировать персептрон и
настроить его веса (неважно, каким образом) так, чтобы он обладал
такой же разделяющей способностью? Если это достижимо, то говорят,
что персептрон способен представлять
желаемую машину. Мы увидим, что возможности представления
однослойными персептронами весьма
ограниченны. Имеется много простых машин, которые не могут быть
представлены персептроном, независимо от
того, как настраиваются его веса.
Проблема функции ИСКЛЮЧАЮЩЕГО ИЛИ
Один из самых пессимистических результатов М.Л. Минского гласит,
что однослойный персептрон не может
воспроизвести такую простую функцию, как ИСКЛЮЧАЮЩЕЕ ИЛИ. Это
функция от двух аргументов, каждый из которых может быть нулем или
единицей. Она принимает значение единицы, когда один из аргументов
равен единице (но не оба). Проблему можно проиллюстрировать с
помощью однослойной однонейронной системы с двумя входами,
показанной на рис.
2.3.

Рис. 2.3.
Обозначим один вход через  , а другой через , а другой через 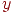 , тогда все их возможные комбинации будут состоять из
четырех точек на плоскости , тогда все их возможные комбинации будут состоять из
четырех точек на плоскости  , как показано на рис.
2.4. Например, точка , как показано на рис.
2.4. Например, точка  и и  обозначена на рисунке как точка обозначена на рисунке как точка 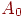 . Табл.
2.1 показывает требуемую связь между входами и выходом, где
входные комбинации, которые должны давать нулевой выход, помечены . Табл.
2.1 показывает требуемую связь между входами и выходом, где
входные комбинации, которые должны давать нулевой выход, помечены
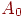 и и 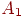 , единичный выход - , единичный выход -  и и  . .
Таблица 2.1.
| Точки |
Значения  |
Значения 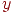 |
Требуемый выход |
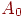 |
0 |
0 |
0 |
 |
1 |
0 |
1 |
 |
0 |
1 |
1 |
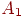 |
1 |
1 |
0 |
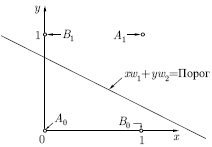
Рис. 2.4.
В сети на рис.
2.3 функция  является обычным порогом, так что OUT принимает значение 0, когда NET меньше 0,5, и 1 в случае, когда NET больше или равно 0,5. Нейрон выполняет
следующее вычисление: является обычным порогом, так что OUT принимает значение 0, когда NET меньше 0,5, и 1 в случае, когда NET больше или равно 0,5. Нейрон выполняет
следующее вычисление:
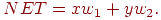 |
(1)
|
Никакая комбинация значений двух весов не может дать соотношения
между входом и выходом, задаваемого табл.
2.1. Чтобы понять это ограничение, зафиксируем  на величине порога 0,5. Сеть в этом случае описывается
уравнением (2). Это уравнение линейно по на величине порога 0,5. Сеть в этом случае описывается
уравнением (2). Это уравнение линейно по  и и 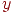 , т. е. все значения по , т. е. все значения по  и и 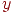 , удовлетворяющие этому уравнению, будут лежать на
некоторой прямой в плоскости , удовлетворяющие этому уравнению, будут лежать на
некоторой прямой в плоскости  . .
 |
(2)
|
Любые входные значения для  и и 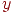 на этой линии будут давать пороговое значение 0,5 для на этой линии будут давать пороговое значение 0,5 для  . Входные значения с одной стороны прямой обеспечат
значения . Входные значения с одной стороны прямой обеспечат
значения  больше порога, следовательно, больше порога, следовательно, 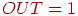 . Входные значения по другую сторону прямой обеспечат
значения NET меньше порога, делая . Входные значения по другую сторону прямой обеспечат
значения NET меньше порога, делая  равным 0. Изменения значений равным 0. Изменения значений  , ,  и порога будут менять наклон и положение прямой. Для того
чтобы сеть реализовала функцию ИСКЛЮЧАЮЩЕЕ ИЛИ, заданную табл.
2.1, нужно расположить прямую так, чтобы точки и порога будут менять наклон и положение прямой. Для того
чтобы сеть реализовала функцию ИСКЛЮЧАЮЩЕЕ ИЛИ, заданную табл.
2.1, нужно расположить прямую так, чтобы точки 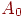 , , 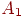 были с одной стороны прямой, а точки были с одной стороны прямой, а точки  , ,  — с другой. Попытавшись нарисовать такую прямую на рис.
2.4, убеждаемся, что это невозможно. Это означает, что какие бы
значения ни приписывались весам и порогу, сеть неспособна
воспроизвести соотношение между входом и выходом, требуемое для
представления функции ИСКЛЮЧАЮЩЕЕ ИЛИ. Взглянув на задачу с другой
точки зрения, рассмотрим — с другой. Попытавшись нарисовать такую прямую на рис.
2.4, убеждаемся, что это невозможно. Это означает, что какие бы
значения ни приписывались весам и порогу, сеть неспособна
воспроизвести соотношение между входом и выходом, требуемое для
представления функции ИСКЛЮЧАЮЩЕЕ ИЛИ. Взглянув на задачу с другой
точки зрения, рассмотрим  как поверхность над плоскостью как поверхность над плоскостью  . Каждая точка этой поверхности находится над
соответствующей точкой плоскости . Каждая точка этой поверхности находится над
соответствующей точкой плоскости  на расстоянии, равном значению на расстоянии, равном значению  в этой точке. Можно показать, что наклон этой в этой точке. Можно показать, что наклон этой  -поверхности одинаков для всей поверхности -поверхности одинаков для всей поверхности  . Все точки, в которых значение . Все точки, в которых значение  равно величине порога, проектируются на линию уровня
плоскости равно величине порога, проектируются на линию уровня
плоскости  (см. рис.2.5). (см. рис.2.5).
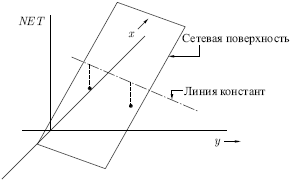
Рис. 2.5.
Ясно, что все точки по одну сторону пороговой прямой проецируются
в значения  большие порога, а точки по другую сторону дадут меньшие
значения большие порога, а точки по другую сторону дадут меньшие
значения  . Таким образом, пороговая прямая разбивает плоскость . Таким образом, пороговая прямая разбивает плоскость  на две области. Во всех точках по одну сторону пороговой
прямой значение на две области. Во всех точках по одну сторону пороговой
прямой значение  равно единице, по другую сторону — нулю. равно единице, по другую сторону — нулю.
Линейная разделимость
Как мы убедились, невозможно нарисовать прямую линию, разделяющую
плоскость  так, чтобы реализовывалась функция ИСКЛЮЧАЮЩЕЕ ИЛИ. К
сожалению, этот пример не единственный. Имеется обширный класс
функций, не реализуемых однослойной сетью. Об этих функциях говорят,
что они являются линейно неразделимыми: они-то и накладывают
определенные ограничения на возможности однослойных сетей. так, чтобы реализовывалась функция ИСКЛЮЧАЮЩЕЕ ИЛИ. К
сожалению, этот пример не единственный. Имеется обширный класс
функций, не реализуемых однослойной сетью. Об этих функциях говорят,
что они являются линейно неразделимыми: они-то и накладывают
определенные ограничения на возможности однослойных сетей.
Линейная разделимость ограничивает
однослойные сети задачами классификации, в которых множества точек
(соответствующих входным значениям) могут быть разделены
геометрически. Для нашего случая с двумя входами разделитель
является прямой линией. В случае трех входов разделение
осуществляется плоскостью, рассекающей трехмерное пространство. Для
четырех или более входов визуализация невозможна, и необходимо
мысленно представить  -мерное пространство, рассекаемое "гиперплоскостью" —
геометрическим объектом, который делит пространство четырех или
большего числа измерений. -мерное пространство, рассекаемое "гиперплоскостью" —
геометрическим объектом, который делит пространство четырех или
большего числа измерений.
Так как линейная разделимость
ограничивает возможности персептронного
представления, то важно знать, является ли данная функция
разделимой. К сожалению, не существует простого способа определить
это, если число переменных велико.
Нейрон с  двоичными входами может иметь двоичными входами может иметь  различных входных образов, состоящих из нулей и единиц.
Так как каждый входной образ может соответствовать двум различным
бинарным выходам (единица и ноль), то всего имеется различных входных образов, состоящих из нулей и единиц.
Так как каждый входной образ может соответствовать двум различным
бинарным выходам (единица и ноль), то всего имеется 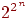 функций от функций от  переменных. переменных.
Таблица 2.2.
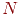 |
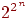 |
Число линейно разделимых
функций |
| 1 |
4 |
4 |
| 2 |
16 |
14 |
| 3 |
256 |
104 |
| 4 |
65536 |
1882 |
| 5 |
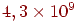 |
94572 |
| 6 |
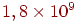 |
15028134 |
Как следует из табл.
2.2, вероятность того, что случайно выбранная функция окажется
линейно разделимой, весьма мала даже для
умеренного числа переменных. По этой причине однослойные персептроны на практике ограничены простыми
задачами.
Преодоление ограничения линейной разделимости
К концу 1960-х годов проблема линейной
разделимости была хорошо понята. К тому же, было известно,
что это серьезное ограничение представляемости однослойными сетями
можно преодолеть, добавив дополнительные слои. Например, двухслойные
сети можно получить каскадным соединением двух однослойных сетей.
Они способны выполнять более общие классификации, отделяя те точки,
которые содержатся в выпуклых ограниченных или неограниченных
областях. Область называется выпуклой, если для любых двух ее точек
соединяющий их отрезок целиком лежит в области. Область называется
ограниченной, если ее можно заключить в некоторый круг.
Неограниченную область невозможно заключить внутрь круга (например,
область между двумя параллельными линиями). Примеры выпуклых
ограниченных и неограниченных областей представлены на рис.
2.6.
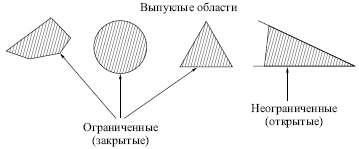
Рис. 2.6.
Чтобы уточнить требование выпуклости, рассмотрим простую
двуслойную сеть с двумя входами, которые подведены к двум нейронам
первого слоя, соединенными с единственным нейроном в слое 2 (см. рис.
2.7а). Пусть порог выходного нейрона равен 0,75, а оба его веса
равны 0,5. В этом случае для того, чтобы порог был превышен и на
выходе появилась единица, требуется, чтобы оба нейрона первого
уровня на выходе имели единицу. Таким образом, выходной нейрон
реализует логическую функцию И. На рис.
2.7а каждый нейрон слоя 1 разбивает плоскость  на две полуплоскости, один обеспечивает единичный выход
для входов ниже верхней линии, другой — для входов выше нижней
линии. На рис.
2.7б показан результат такого двойного разбиения, где выходной
сигнал нейрона второго слоя равен единице только внутри на две полуплоскости, один обеспечивает единичный выход
для входов ниже верхней линии, другой — для входов выше нижней
линии. На рис.
2.7б показан результат такого двойного разбиения, где выходной
сигнал нейрона второго слоя равен единице только внутри 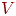 -образной области. Аналогично, во втором слое может быть
использовано три нейрона с дальнейшим разбиением плоскости и
созданием области треугольной формы. Включением достаточного числа
нейронов во входной слой может быть образован выпуклый многоугольник
любой желаемой формы. Все такие многогранники выпуклы, так как они
образованы с помощью операции И над областями, задаваемыми линиями:
следовательно, только выпуклые области и возникают. Точки, не
составляющие выпуклой области, не могут быть отделены от других
точек плоскости двухслойной сетью. -образной области. Аналогично, во втором слое может быть
использовано три нейрона с дальнейшим разбиением плоскости и
созданием области треугольной формы. Включением достаточного числа
нейронов во входной слой может быть образован выпуклый многоугольник
любой желаемой формы. Все такие многогранники выпуклы, так как они
образованы с помощью операции И над областями, задаваемыми линиями:
следовательно, только выпуклые области и возникают. Точки, не
составляющие выпуклой области, не могут быть отделены от других
точек плоскости двухслойной сетью.
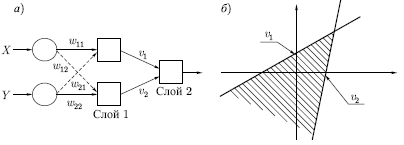
Рис. 2.7.
Нейрон второго слоя не ограничен функцией И. Он может
реализовывать многие другие функции при подходящем выборе весов и
порога. Например, можно сделать так, чтобы единичный выход любого из
нейронов первого слоя приводил к появлению единицы на выходе нейрона
второго слоя, реализовав тем самым логическое ИЛИ. Например, имеется
16 двоичных функций от двух переменных. Если выбирать подходящим
образом веса и порог, то можно воспроизвести 14 из них (все, кроме
ИСКЛЮЧАЮЩЕЕ ИЛИ и ИСКЛЮЧАЮЩЕЕ НЕТ).
Входы не обязательно должны быть двоичными. Вектор непрерывных
входов может представлять собой произвольную точку на плоскости  . В этом случае мы имеем дело со способностью сети
разбивать плоскость на непрерывные области, а не с разделением
дискретных множеств точек. Для всех этих функций, однако, линейная разделимость показывает, что выход
нейрона второго слоя равен единице только в части плоскости . В этом случае мы имеем дело со способностью сети
разбивать плоскость на непрерывные области, а не с разделением
дискретных множеств точек. Для всех этих функций, однако, линейная разделимость показывает, что выход
нейрона второго слоя равен единице только в части плоскости  , ограниченной многоугольной областью. Поэтому для
разделения плоскостей , ограниченной многоугольной областью. Поэтому для
разделения плоскостей  и и  необходимо, чтобы все необходимо, чтобы все  лежали внутри выпуклой многоугольной области, не
содержащей точек лежали внутри выпуклой многоугольной области, не
содержащей точек  (или наоборот). (или наоборот).
Трехслойная сеть, впрочем, есть более общий случай. Ее
классифицирующие возможности ограничены лишь числом искусственных
нейронов и весов. Ограничения на выпуклость отсутствуют. Теперь
нейрон третьего слоя принимает в качестве входа набор выпуклых
многоугольников, и их логическая комбинация может быть невыпуклой.
На рис.
2.8б иллюстрируется ситуация, когда два треугольника A и B,
скомбинированные с помощью функций "A и не B", задают невыпуклую
область. При добавлении нейронов и весов число сторон
многоугольников может неограниченно возрастать. Это позволяет
аппроксимировать область любой формы с любой точностью. Вдобавок, не
все выходные области второго слоя должны пересекаться. Возможно,
следовательно, объединять различные области, выпуклые и невыпуклые,
выдавая на выходе единицу всякий раз, когда входной вектор
принадлежит одной из них.
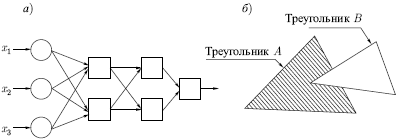
Рис. 2.8.
Несмотря на то, что возможности многослойных сетей были известны
давно, в течение многих лет не было теоретически обоснованного
алгоритма для настройки их весов. В последующих главах мы детально
изучим многослойные обучающие алгоритмы, но сейчас достаточно
понимать суть проблемы и знать, что исследования привели к
определенным результатам.
Эффективность запоминания
Серьезные вопросы существуют относительно эффективности
запоминания информации в персептроне (или
любых других нейронных сетях) по сравнению с обычной компьютерной
памятью и методами поиска информации в ней. Например, в компьютерной
памяти можно хранить все входные образы вместе с классифицирующими
битами. Компьютер должен найти требуемый образ и дать его
классификацию. Многочисленные и хорошо известные методы могли бы
применяться для ускорения поиска. Если точное соответствие не
найдено, то для ответа может быть использовано правило ближайшего
соседа.
Число битов, необходимое для хранения этой же информации в весах
персептрона, может быть значительно
меньшим по сравнению с методом обычной компьютерной памяти, если
образы допускают экономичную запись. Однако М.Л.Минский построил
патологические примеры, в которых число битов, требуемых для
представления весов, растет в зависимости от размерности задачи
быстрее, чем экспоненциально. В этих случаях требования к памяти
быстро становятся невыполнимыми. Если, как он предположил, эта
ситуация не является исключением, то персептроны часто могут быть ограничены только
малыми задачами. Насколько общими являются такие неподатливые
множества образов? Вопрос остается открытым и относится ко всем
нейронным сетям. Поиски ответа чрезвычайно важны для дальнейших
исследований в этой области.
|




