Обучение персептрона
Способность искусственных нейронных сетей к обучению является их
наиболее интригующим свойством. Подобно биологическим системам,
которые они моделируют, эти нейронные сети сами совершенствуют себя
в результате попыток создать лучшую модель поведения.
Используя критерий линейной разделимости, можно решить, способна
ли однослойная нейронная сеть реализовывать требуемую функцию. Даже
в том случае, когда ответ положительный, это принесет мало пользы,
если у нас нет способа найти нужные значения для весов и порогов.
Чтобы сеть представляла практическую ценность, нужен систематический
метод (алгоритм) для вычисления этих значений. Ф.Розенблатт создал
такой метод в своем алгоритме обучения
персептрона и доказал: персептрон
может быть обучен всему, что он может реализовывать.
Обучение может быть с учителем или без него. Для обучения с
учителем нужен "внешний" учитель, который оценивал бы поведение
системы и управлял ее последующими модификациями. При обучении без
учителя, которое будет рассмотрено на последующих лекциях, сеть
путем самоорганизации делает требуемые изменения. Обучение персептрона является обучением с учителем.
Алгоритм обучения персептрона может
быть реализован на цифровом компьютере или другом электронном
устройстве, и сеть становится в определенном смысле
самоподстраивающейся. По этой причине процедуру подстройки весов
обычно называют "обучением" и говорят, что сеть "обучается".
Доказательство Розенблатта стало основной вехой и дало мощный
импульс исследованиям в этой области. Сегодня в той или иной форме
элементы алгоритма обучения персептрона
встречаются во многих сетевых парадигмах.
Алгоритм обучения однослойного персептрона
Персептрон должен решать задачу
классификации по бинарным входным сигналам. Набор входных сигналов
будем обозначать  -мерным вектором -мерным вектором  . Все элементы вектора являются булевыми переменными
(переменными, принимающими значения "Истина" или "Ложь"). Однако
иногда полезно оперировать числовыми значениями. Будем считать, что
значению "ложь" соответствует числовое значение 0, а значению
"Истина" соответствует 1. . Все элементы вектора являются булевыми переменными
(переменными, принимающими значения "Истина" или "Ложь"). Однако
иногда полезно оперировать числовыми значениями. Будем считать, что
значению "ложь" соответствует числовое значение 0, а значению
"Истина" соответствует 1.
Персептроном будем называть
устройство, вычисляющее следующую систему функций:
![\psi=\Bigl[\sum_{i=1}^m w_{ij} x_I>\theta\Bigr],\quad j=1,\ldots, n,](a8ec638de3fbfca8166469ed534245a5.png) |
(1)
|
где  — веса персептрона, — веса персептрона,  — порог, — порог,  — значения входных сигналов, скобки — значения входных сигналов, скобки ![[]](93cccb41cdc2040c49447ce479e6f63e.png) означают переход от булевых (логических) значений к
числовым значениям по правилам, изложенным выше. означают переход от булевых (логических) значений к
числовым значениям по правилам, изложенным выше.
Обучение персептрона состоит в
подстройке весовых коэффициентов. Пусть имеется набор пар векторов
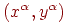 , , 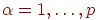 , называемый обучающей выборкой. Будем называть
нейронную сеть обученной на данной обучающей выборке, если при
подаче на входы сети каждого вектора , называемый обучающей выборкой. Будем называть
нейронную сеть обученной на данной обучающей выборке, если при
подаче на входы сети каждого вектора 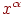 на выходах всякий раз получается соответствующий вектор на выходах всякий раз получается соответствующий вектор
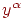 . .
Предложенный Ф.Розенблаттом метод обучения состоит в итерационной
подстройке матрицы весов, последовательно уменьшающей ошибку в
выходных векторах. Алгоритм включает несколько шагов:
| Шаг 0 |
Начальные значения весов всех
нейронов 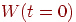 полагаются случайными полагаются случайными |
| Шаг 1 |
Сети предъявляется входной
образ 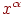 , в результате формируется выходной образ , в результате формируется выходной образ 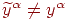 . . |
| Шаг 2 |
Вычисляется вектор ошибки 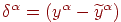 , делаемой сетью на выходе. Дальнейшая идея состоит
в том, что изменение вектора весовых коэффициентов в области
малых ошибок должно быть пропорционально ошибке на выходе и
равно нулю, если ошибка равна нулю. , делаемой сетью на выходе. Дальнейшая идея состоит
в том, что изменение вектора весовых коэффициентов в области
малых ошибок должно быть пропорционально ошибке на выходе и
равно нулю, если ошибка равна нулю. |
| Шаг 3 |
Вектор весов модифицируется по
следующей формуле: 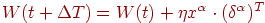 . Здесь . Здесь 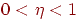 — темп обучения. — темп обучения. |
| Шаг 4 |
Шаги 1—3 повторяются для всех
обучающих векторов. Один цикл последовательного предъявления
всей выборки называется эпохой. Обучение завершается по
истечении нескольких эпох: а) когда итерации сойдутся, т.е.
вектор весов перестает изменяться, или б) когда полная,
просуммированная по всем векторам абсолютная ошибка станет
меньше некоторого малого значения. |
Объясним данный алгоритм более подробно. Подаем на вход персептрона такой вектор  , для которого уже известен правильный ответ. Если выходной
сигнал персептрона совпадает с правильным
ответом, то никаких действий предпринимать не надо. В случае ошибки,
необходимо обучить персептрон правильно
решать данный пример. Ошибки могут быть двух типов. Рассмотрим
каждый из них. , для которого уже известен правильный ответ. Если выходной
сигнал персептрона совпадает с правильным
ответом, то никаких действий предпринимать не надо. В случае ошибки,
необходимо обучить персептрон правильно
решать данный пример. Ошибки могут быть двух типов. Рассмотрим
каждый из них.
Первый тип ошибки: на выходе персептрона — 0, а правильный ответ — 1. Для
того чтобы персептрон выдавал правильный
ответ, необходимо, чтобы сумма в правой части (1) стала больше.
Поскольку переменные принимают значения 0 или 1, увеличение суммы
может быть достигнуто за счет увеличения весов  . Однако нет смысла увеличивать веса при переменных . Однако нет смысла увеличивать веса при переменных 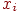 , которые равны нулю. Таким образом, следует увеличить веса , которые равны нулю. Таким образом, следует увеличить веса
 при тех переменных xi, которые равны 1. при тех переменных xi, которые равны 1.
Первое правило. Если на выходе персептрона получен 0, а правильный ответ равен
1, то необходимо увеличить веса связей между одновременно активными
нейронами. При этом выходной персептрон
считается активным. Второй тип ошибки: на выходе персептрона — 1, а правильный ответ равен нулю.
Для обучения правильному решению данного примера следует уменьшить
сумму в правой части (1). Следовательно, необходимо уменьшить веса
связей  при тех переменных, которые равны 1 (поскольку нет смысла
уменьшать веса связей при равных нулю переменных~ при тех переменных, которые равны 1 (поскольку нет смысла
уменьшать веса связей при равных нулю переменных~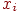 ). Необходимо также провести эту процедуру для всех
активных нейронов предыдущих слоев. В результате получаем второе
правило. ). Необходимо также провести эту процедуру для всех
активных нейронов предыдущих слоев. В результате получаем второе
правило.
Второе правило. Если на выходе персептрона получена единица, а правильный
ответ равен нулю, то необходимо уменьшить веса связей между
одновременно активными нейронами.
Таким образом, процедура обучения сводится к последовательному
перебору всех примеров обучающего множества с применением правил
обучения для ошибочно решенных примеров. Если после очередного цикла
предъявления всех примеров окажется, что все они решены правильно,
то процедура обучения завершается.
Нерассмотренными остались два вопроса. Первый — о сходимости
процедуры обучения. Второй — на сколько нужно увеличивать
(уменьшать) веса связей при применении правил обучения.
Ответ на первый вопрос дают следующие теоремы.
Теорема о сходимости персептрона. Если существует вектор параметров
 , при котором персептрон
правильно решает все примеры обучающей выборки, то при обучении
персептрона по вышеописанному алгоритму
решение будет найдено за конечное число шагов. , при котором персептрон
правильно решает все примеры обучающей выборки, то при обучении
персептрона по вышеописанному алгоритму
решение будет найдено за конечное число шагов.
Теорема о "зацикливании" персептрона. Если не существует вектора
параметров  , при котором персептрон
правильно решает все примеры обучающей выборки, то при обучении
персептрона по данному правилу через
конечное число шагов вектор весов начнет повторяться. , при котором персептрон
правильно решает все примеры обучающей выборки, то при обучении
персептрона по данному правилу через
конечное число шагов вектор весов начнет повторяться.
Таким образом, данные теоремы утверждают, что, запустив процедуру
обучения персептрона, через конечное
время мы либо получим обучившийся персептрон, либо ответ, что данный персептрон поставленной задаче обучится не
может.
Доказательства этих теорем в данное учебное пособие не
включены.
Целочисленность весов персептронов
Для ответа на вопрос о количественных характеристиках вектора
w рассмотрим следующую теорему.
Теорема. Любой персептрон можно
заменить другим персептроном того же вида
с целыми весами связей.
Доказательство.Обозначим множество примеров одного класса
(правильный ответ равен 0) через 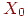 , а другого (правильный ответ равен 1) — через , а другого (правильный ответ равен 1) — через  . Вычислим максимальное и минимальное значения суммы в
правой части (1): . Вычислим максимальное и минимальное значения суммы в
правой части (1):
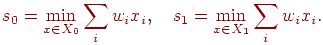
Определим допуск 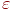 как минимум из как минимум из  и и  . Положим . Положим 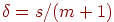 , где , где  — число слагаемых в (1). Поскольку персептрон(1) решает поставленную задачу
классификации и множество примеров в обучающей выборке конечно, то — число слагаемых в (1). Поскольку персептрон(1) решает поставленную задачу
классификации и множество примеров в обучающей выборке конечно, то
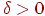 . Из теории чисел известна теорема о том, что любое
действительное число можно сколь угодно точно приблизить
рациональными числами. Заменим веса . Из теории чисел известна теорема о том, что любое
действительное число можно сколь угодно точно приблизить
рациональными числами. Заменим веса  на рациональные числа так, чтобы выполнялись следующие
неравенства: на рациональные числа так, чтобы выполнялись следующие
неравенства: 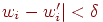 . .
Из этих неравенств следует, что при использовании весов 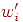 персептрон будет работать с
теми же результатами, что и первоначальный персептрон. Действительно, если правильным
ответом примера является 0, имеем персептрон будет работать с
теми же результатами, что и первоначальный персептрон. Действительно, если правильным
ответом примера является 0, имеем 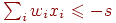 . .
Подставив новые веса, получим:
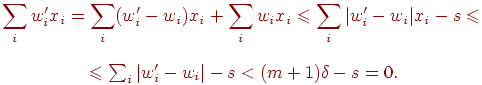
Откуда следует необходимое неравенство
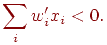 |
(2)
|
Аналогично, в случае правильного ответа равного 1, имеем 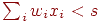 , откуда, подставив новые веса и порог, получим: , откуда, подставив новые веса и порог, получим:
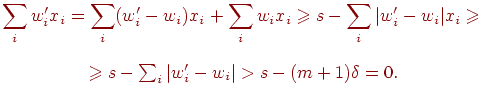
Отсюда следует выполнение неравенства
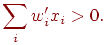 |
(3)
|
Неравенства (2) и (3) доказывают возможность замены всех весов и
порога любого персептрона рациональными
числами. Очевидно также, что при умножении всех весов и порога на
одно и то же ненулевое число персептрон
не изменится. Поскольку любое рациональное число можно представить в
виде отношения целого числа к натуральному числу, получим
![\psi=\Bigl[\sum_{i=1}^m w_i x_i>0\Bigr]= \Bigl[\sum_{i=1}^m w_i'
x_i>0\Bigr]= \Bigl[\sum_{i=1}^m \frac{w_i''}{r_i} x_i>0\Bigr],](3eb30fa8804b38a58a788ba622b733f9.png) |
(4)
|
где  — целые числа. Обозначим через — целые числа. Обозначим через  произведение всех знаменателей: произведение всех знаменателей: . Умножим все веса и порог на . Умножим все веса и порог на  . Получим веса целочисленные . Получим веса целочисленные  . Из (2), (3) и (4) получаем . Из (2), (3) и (4) получаем
![\psi=\Bigl[\sum_{i=1}^m w_i x_i>0\Bigr]=
\Bigl[\sum_{i=1}^m w_i' x_i>0\Bigr]=
\Bigl[\sum_{i=1}^m \frac{w_i''}{r_i} x_i>0\Bigr]=
\Bigl[\sum_{i=1}^m w_i''' x_i>0\Bigr],](876efdb6faf3edd3d060395a6230e05f.png)
что и завершает доказательство теоремы.
Поскольку из доказанной теоремы следует, что веса персептрона являются целыми числами, то вопрос
о выборе шага при применении правил обучения решается просто: веса и
порог следует увеличивать (уменьшать) на единицу.
Двуслойность персептрона
Как уже упоминалось в начале лекции, алгоритм
обучения персептрона возможно использовать и для многослойных
персептронов. Однако теоремы о сходимости
и зацикливании персептрона, приведенные
выше, верны только при обучении однослойного персептрона — или многослойного персептрона при условии, что обучаются только
веса персептрона, стоящего в последнем
слое сети. В случае произвольного многослойного персептрона они не работают. Следующий пример
демонстрирует основную проблему, возникающую при обучении
многослойных персептронов.
Пусть веса всех слоев персептрона в
ходе обучения сформировались так, что все примеры обучающего
множества, кроме первого, решаются правильно. При этом правильным
ответом первого примера является 1. Все входные сигналы персептрона последнего слоя равны нулю. В этом
случае первое правило не дает результата, поскольку все нейроны
предпоследнего слоя не активны. Существует множество способов решать
эту проблему. Однако все эти методы не являются регулярными и не
гарантируют сходимость многослойного персептрона к решению, даже при условии, что
такое решение существует.
В действительности, проблема настройки (обучения) многослойного
персептрона решается следующей
теоремой.
Теорема о двуслойности персептрона. Любой многослойный персептрон может быть представлен в виде
двуслойного персептрона с необучаемыми
весами первого слоя.
Для доказательства этой теоремы потребуется одна теорема из
математической логики.
Теорема о дизъюнктивной нормальной форме. Любая булева
функция булевых аргументов может быть представлена в виде дизъюнкции
конъюнкций элементарных высказываний и отрицаний элементарных
высказываний: 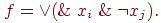
Напомним некоторые свойства дизъюнктивной нормальной формы.
Свойство 1. В каждый конъюнктивный член (слагаемое) входят все
элементарные высказывания либо в виде самого высказывания, либо в
виде его отрицания.
Свойство 2. При любых значениях элементарных высказываний в
дизъюнктивной нормальной форме может быть истинным не более одного
конъюнктивного члена (слагаемого).
Доказательство теоремы о двуслойности персептрона. Из теоремы о дизъюнктивной
нормальной форме следует, что любой многослойный персептрон может быть представлен в следующем
виде:
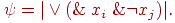 |
(5)
|
В силу второго свойства дизъюнктивной нормальной формы, равенство
(5) можно переписать в виде
![\psi=[\vee(\&\;x_i\;\&\;\neg x_j)]=\left[\sum[(\&\;x_i\;\&\;\neg
x_j)]>0\right].](7d6782b932b94b7cff6d148c958b3fb6.png) |
(6)
|
Переведем в арифметическую форму все слагаемые в выражении (6).
Конъюнкцию заменяем на умножение, а отрицание на разность: 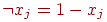 . Произведя эту замену и приведя подобные члены,
получим: . Произведя эту замену и приведя подобные члены,
получим:
![\psi=\left[\sum_l \alpha_l\prod_{i\in I_l}x_i>0\right],](a359d1c3468b5701eea43f59ef563b5c.png) |
(7)
|
где 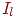 — множество индексов сомножителей в — множество индексов сомножителей в  -м слагаемом, -м слагаемом,  — число, указывающее, сколько раз такое слагаемое
встретилось в выражении (6) после замены и раскрытия скобок (число
подобных слагаемых). — число, указывающее, сколько раз такое слагаемое
встретилось в выражении (6) после замены и раскрытия скобок (число
подобных слагаемых).
Заменим  -е слагаемое в формуле (7) персептроном следующего вида: -е слагаемое в формуле (7) персептроном следующего вида:
![\varphi_i=\prod_{l\in I_l} x_l=\left[\sum_{l\in I_l}x_l>|I_l|-1\right].](86eb903d6fa4d955a1ada791fbe0bd63.png) |
(8)
|
Подставив выражение (8) в формулу (7), получим равенство (1), то
есть произвольный многослойный персептрон
представлен в виде (1) с целочисленными коэффициентами. В качестве
персептронов первого слоя используются
персептроны вида (8) с необучаемыми
весами. Теорема доказана.
Подводя итоги данной лекции, следует отметить следующие основные
свойства персептронов:
- Любой персептрон может содержать
один или два слоя. В случае двухслойного персептрона веса первого слоя не обучаются.
- Веса любого персептрона можно
заменить на целочисленные.
- При обучении после конечного числа итераций возможны два
исхода: персептрон обучится или вектор
весов персептрона будет повторяться
(персептрон зациклится).
Знание этих свойств позволяет избежать "усовершенствований" типа
модификации скорости обучения и других, столь же "эффективных"
модернизаций.
Трудности с алгоритмом обучения персептрона
Иногда бывает сложно определить, выполнено ли условие
разделимости для конкретного обучающего множества. Кроме того, во
многих встречающихся на практике ситуациях входы часто меняются во
времени и могут быть разделимы в один момент времени и неразделимы -
в другой. В доказательстве алгоритма обучения
персептрона ничего не говорится также о том, сколько шагов
требуется для обучения сети. Мало утешительного знать, что обучение
закончится за конечное число шагов, если необходимое для этого время
сравнимо с геологической эпохой. Кроме того, не доказано, что персептронный алгоритм обучения более быстр по
сравнению с простым перебором всех возможных значений весов, и в
некоторых случаях этот примитивный подход может оказаться лучше.
На эти вопросы никогда не находилось удовлетворительного ответа,
они относятся к природе обучающего материала. В различной форме они
возникнут на последующих лекциях, где рассматриваются другие сетевые
парадигмы. Ответы для современных сетей, как правило, не более
удовлетворительны, чем для персептрона.
Эти проблемы являются важной областью современных
исследований.
|




