Введение в процедуру обратного распространения
Среди различных структур нейронных сетей (НС) одной из наиболее
известных является многослойная структура, в которой каждый нейрон
произвольного слоя связан со всеми аксонами нейронов предыдущего
слоя или, в случае первого слоя, со всеми входами НС. Такие НС
называются полносвязными. Когда в сети только один слой, алгоритм ее
обучения с учителем довольно очевиден, так как правильные выходные
состояния нейронов единственного слоя заведомо известны и подстройка
синаптических связей идет в направлении, минимизирующем ошибку на
выходе сети. По этому принципу строится, например, алгоритм обучения
однослойного персептрона. В многослойных же сетях оптимальные
выходные значения нейронов всех слоев, кроме последнего, как
правило, не известны, и двух- или более слойный персептрон уже
невозможно обучить, руководствуясь только величинами ошибок на
выходах НС.
Один из вариантов решения этой проблемы — разработка наборов
выходных сигналов, соответствующих входным, для каждого слоя НС,
что, конечно, является очень трудоемкой операцией и не всегда
осуществимо. Второй вариант — динамическая подстройка весовых
коэффициентов синапсов, в ходе которой выбираются, как правило,
наиболее слабые связи и изменяются на малую величину в ту или иную
сторону, а сохраняются только те изменения, которые повлекли
уменьшение ошибки на выходе всей сети. Очевидно, что данный "метод
тыка", несмотря на свою кажущуюся простоту, требует громоздких
рутинных вычислений. И, наконец, третий, более приемлемый вариант —
распространение сигналов ошибки от выходов НС к ее входам, в
направлении, обратном прямому распространению сигналов в обычном
режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения.
Разработка алгоритма обратного
распространения сыграла важную роль в возрождении интереса к
искусственным нейронным сетям. Обратное распространение — это
систематический метод для обучения многослойных искусственных
нейронных сетей. Он имеет солидное математическое обоснование.
Несмотря на некоторые ограничения, процедура
обратного распространения сильно расширила область проблем, в
которых могут быть использованы искусственные нейронные сети, и
убедительно продемонстрировала богатые возможности этой
методики.
Обучающий алгоритм обратного распространения
Сетевые конфигурации:
Нейрон. На рис.
4.1 показан нейрон, используемый в качестве основного
строительного блока в сетях обратного
распространения. Подается множество входов, идущих либо
извне, либо от предшествующего слоя. Каждый из них умножается на
вес, и произведения суммируются: 
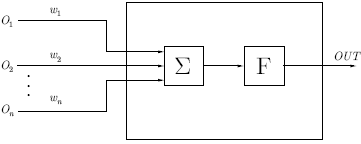
Рис. 4.1.
Эта сумма, обозначаемая  , должна быть вычислена для каждого нейрона сети. После
того, как величина , должна быть вычислена для каждого нейрона сети. После
того, как величина  вычислена, она модифицируется с помощью активационной функции, и
получается сигнал OUT. Для алгоритмов обратного
распространения обычно используется функция
вычислена, она модифицируется с помощью активационной функции, и
получается сигнал OUT. Для алгоритмов обратного
распространения обычно используется функция
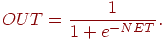 |
(1)
|
Как показывает уравнение (1), эта функция, называемая
сигмоидом, весьма удобна, так как имеет простую производную,
что используется при реализации алгоритма
обратного распространения:
 |
(2)
|
Сигмоид, который иногда называется также логистической или
сжимающей функцией, сужает диапазон изменения  так, что значение
так, что значение  лежит между нулем и единицей. Как указывалось выше, многослойные
нейронные сети обладают большей представляющей мощностью, чем
однослойные, лишь в случае присутствия нелинейности. Сжимающая
функция обеспечивает требуемую нелинейность.
лежит между нулем и единицей. Как указывалось выше, многослойные
нейронные сети обладают большей представляющей мощностью, чем
однослойные, лишь в случае присутствия нелинейности. Сжимающая
функция обеспечивает требуемую нелинейность.
В действительности имеется множество функций, которые могли бы
быть использованы. Для алгоритма обратного
распространения требуется только, чтобы функция была всюду
дифференцируема. Сигмоид удовлетворяет этому требованию. Его
дополнительное преимущество состоит в автоматическом контроле
усиления. Для слабых сигналов (величина NET близка к нулю) кривая вход-выход имеет
сильный наклон, дающий большое усиление. Когда величина сигнала
становится больше, усиление падает. Таким образом, большие сигналы
воспринимаются сетью без насыщения, а слабые сигналы проходят по
сети без чрезмерного ослабления. Многослойная сеть. Рассмотрим
иерархическую сетевую структуру, в которой связанные между собой
нейроны объединены в несколько слоев (см. рис.
4.2). На возможность построения таких архитектур указал еще
Ф.Розенблатт, однако им не была решена проблема обучения.
Межнейронные синаптические связи сети устроены таким образом, что
каждый нейрон на данном уровне иерархии принимает и обрабатывает
сигналы от каждого нейрона более низкого уровня. Таким образом, в
данной сети имеется выделенное направление распространения
нейроимпульсов — от входного слоя через один (или несколько) скрытых
слоев к выходному слою нейронов. Нейросеть такой топологии мы будем
называть обобщенным многослойным персептроном или, если это
не будет вызывать недоразумений, просто персептроном.
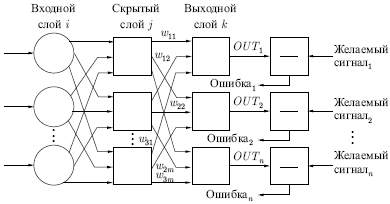
Рис. 4.2.
Персептрон представляет собой сеть, состоящую из нескольких
последовательно соединенных слоев нейронов. На низшем уровне
иерархии находится входной слой сенсорных элементов, задачей
которого является только прием и распространение по сети входной
информации. Далее имеются один или, реже, несколько скрытых
слоев. Каждый нейрон на скрытом слое имеет несколько входов,
соединенных с выходами нейронов предыдущего слоя или непосредственно
со входными сенсорами  , и один
выход. Выходы нейронов последнего, выходного, слоя описывают
результат классификации , и один
выход. Выходы нейронов последнего, выходного, слоя описывают
результат классификации 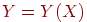 . Особенности работы персептрона состоят в следующем.
Каждый нейрон суммирует поступающие к нему сигналы от нейронов
предыдущего уровня иерархии с весами, определяемыми состояниями
синапсов, и формирует ответный сигнал (переходит в возбужденное
состояние), если полученная сумма выше порогового значения.
Персептрон переводит входной образ, определяющий степени возбуждения
нейронов самого нижнего уровня иерархии, в выходной образ,
определяемый нейронами самого верхнего уровня. Число последних
обычно сравнительно невелико. Состояние возбуждения нейрона на
верхнем уровне говорит о принадлежности входного образа к той или
иной категории. . Особенности работы персептрона состоят в следующем.
Каждый нейрон суммирует поступающие к нему сигналы от нейронов
предыдущего уровня иерархии с весами, определяемыми состояниями
синапсов, и формирует ответный сигнал (переходит в возбужденное
состояние), если полученная сумма выше порогового значения.
Персептрон переводит входной образ, определяющий степени возбуждения
нейронов самого нижнего уровня иерархии, в выходной образ,
определяемый нейронами самого верхнего уровня. Число последних
обычно сравнительно невелико. Состояние возбуждения нейрона на
верхнем уровне говорит о принадлежности входного образа к той или
иной категории.
Традиционно рассматривается аналоговая логика, при которой
допустимые состояния синаптических связей определяются произвольными
действительными числами, а степени активности нейронов -
действительными числами между 0 и 1. Иногда исследуются также модели
с дискретной арифметикой, в которой синапс характеризуется двумя
булевыми переменными: активностью (0 или 1) и полярностью ( или или  ). Состояния нейронов могут при этом описываться одной
булевой переменной. Данный дискретный подход делает конфигурационное
пространство состояний нейронной сети конечным (не говоря уже о
преимуществах при аппаратной реализации). ). Состояния нейронов могут при этом описываться одной
булевой переменной. Данный дискретный подход делает конфигурационное
пространство состояний нейронной сети конечным (не говоря уже о
преимуществах при аппаратной реализации).
Мы рассмотрим классический вариант многослойной сети с
аналоговыми синапсами и сигмоидальной передаточной функцией
нейронов, определяемой формулой (1).
В литературе нет единого мнения относительно того, что именно
считать числом слоев в таких сетях. Одни авторы используют число
слоев нейронов (включая несуммирующий входной слой), другие — число
слоев весов. Так как последнее определение - функционально
описательное, то оно будет использовано и нами. Согласно этому
определению, сеть на рис.
4.2 рассматривается как двухслойная. Нейрон объединен с
множеством весов, присоединенных к его входу. Таким образом, веса
первого слоя оканчиваются на нейронах первого слоя. Вход
распределительного слоя считается нулевым слоем.
Процедура обратного распространения
применима к сетям с любым числом слоев. Однако для того, чтобы
продемонстрировать алгоритм, достаточно двух слоев. Сейчас будут
рассматриваться лишь сети прямого действия, хотя обратное
распространение применимо и к сетям с обратными связями. Эти случаи
будут рассмотрены в данной главе позднее.
Обзор обучения. Целью обучения сети является такая
подстройка ее весов, чтобы приложение некоторого множества входов
приводило к требуемому множеству выходов. Для краткости эти
множества входов и выходов будут называться векторами. При
обучении предполагается, что для каждого входного вектора существует
парный ему целевой вектор, задающий требуемый выход. Вместе они
называются обучающей парой. Как правило, сеть обучается на
многих парах. Например, входная часть обучающей пары может состоять
из набора нулей и единиц, представляющего двоичный образ некоторой
буквы алфавита. На рис.
4.3 показано множество входов для буквы "А", нанесенной на
сетке. Если через квадрат проходит линия, то соответствующий
нейронный вход равен единице, в противном случае он равен нулю.
Выход может быть числом, представляющим букву "А", или другим
набором из нулей и единиц, который может быть использован для
получения выходного образа. При необходимости распознавать с помощью
сети все буквы латинского алфавита, потребовалось бы 26 обучающих
пар. Такая группа обучающих пар называется обучающим
множеством.
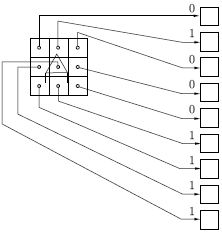
Рис. 4.3.
Перед началом обучения всем весам должны быть присвоены небольшие
начальные значения, выбранные случайным образом. Это гарантирует,
что в сети не произойдет насыщения большими значениями весов, и
предотвращает ряд других некорректных случаев. Например, если всем
весам придать одинаковые начальные значения, а для требуемого
функционирования нужны неравные значения, то сеть не сможет
обучиться.
Обучение сети обратного
распространения требует выполнения следующих операций:
- Выбрать очередную обучающую пару из обучающего множества;
подать входной вектор на вход сети.
- Вычислить выход сети.
- Вычислить разность между выходом сети и требуемым выходом
(целевым вектором обучающей пары).
- Подкорректировать веса сети так, чтобы минимизировать ошибку.
- Повторять шаги с 1 по 4 для каждого вектора обучающего
множества до тех пор, пока ошибка на всем множестве не достигнет
приемлемого уровня.
Операции, выполняемые шагами 1 и 2, сходны с теми, которые
выполняются при функционировании уже обученной сети, — подается
входной вектор и вычисляется получающийся выход. Вычисления
выполняются послойно. На рис.
4.2 сначала вычисляются выходы нейронов слоя 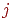 ,
затем они используются в качестве входов слоя ,
затем они используются в качестве входов слоя  ,
после чего вычисляются выходы нейронов слоя ,
после чего вычисляются выходы нейронов слоя  ,
которые и образуют выходной вектор сети. ,
которые и образуют выходной вектор сети.
На шаге 3 каждый из выходов сети, которые на рис.
4.2 обозначены  , вычитается из соответствующей компоненты целевого
вектора, чтобы получить значение ошибки. Эта ошибка используется на
шаге 4 для коррекции весов сети, причем знак и величина изменений
весов определяются алгоритмом обучения (см. ниже). , вычитается из соответствующей компоненты целевого
вектора, чтобы получить значение ошибки. Эта ошибка используется на
шаге 4 для коррекции весов сети, причем знак и величина изменений
весов определяются алгоритмом обучения (см. ниже).
После достаточного числа повторений этих четырех шагов разность
между действительными и целевыми выходами должна уменьшиться до
приемлемой величины: при этом говорят, что сеть обучилась. Теперь
сеть используется для распознавания, и веса не изменяются.
На шаги 1 и 2 можно смотреть как на "проход вперед", так как
сигнал распространяется по сети от входа к выходу. Шаги 3, 4
составляют "обратный проход", здесь вычисляемый сигнал ошибки
распространяется обратно по сети и используется для подстройки
весов. Эти два прохода теперь будут детализированы и записаны как
математические выражения.
Проход вперед. Шаги 1 и 2 могут быть выражены в векторной
форме следующим образом: подается входной вектор  и
на выходе получается вектор и
на выходе получается вектор  .
Векторная пара вход — цель .
Векторная пара вход — цель  и и
 берется из обучающего множества. Вычисления проводятся над вектором
берется из обучающего множества. Вычисления проводятся над вектором
 ,
чтобы получить выходной вектор ,
чтобы получить выходной вектор  . .
Как мы видели, вычисления в многослойных сетях выполняются слой
за слоем, начиная с ближайшего к входу. Величина  каждого нейрона первого слоя вычисляется как взвешенная сумма входов
нейрона. Затем активационная функция
каждого нейрона первого слоя вычисляется как взвешенная сумма входов
нейрона. Затем активационная функция  "сжимает"
"сжимает"  и дает величину и дает величину  для каждого нейрона в этом слое. Когда множество выходов слоя
получено, оно является входным множеством для следующего слоя.
Процесс повторяется слой за слоем, пока не будет получено
заключительное множество выходов сети.
для каждого нейрона в этом слое. Когда множество выходов слоя
получено, оно является входным множеством для следующего слоя.
Процесс повторяется слой за слоем, пока не будет получено
заключительное множество выходов сети.
Этот процесс может быть выражен в сжатой форме с помощью
векторной нотации. Веса между нейронами будем рассматривать как
матрицу 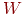 . Например, вес от нейрона 8 в слое 2 к нейрону 5 слоя 3
обозначается . Например, вес от нейрона 8 в слое 2 к нейрону 5 слоя 3
обозначается  . Тогда . Тогда  -вектор слоя -вектор слоя 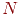 может быть выражен не как сумма произведений, а как произведение
может быть выражен не как сумма произведений, а как произведение
 и и
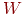 .
В векторном обозначении .
В векторном обозначении 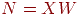 . Покомпонентным применением функции . Покомпонентным применением функции  к к
 -вектору -вектору 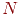 получаем выходной вектор
получаем выходной вектор  .
Таким образом, для данного слоя вычислительный процесс описывается
следующим выражением: .
Таким образом, для данного слоя вычислительный процесс описывается
следующим выражением:
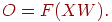 |
(3)
|
Выходной вектор одного слоя является входным вектором для
следующего, поэтому вычисление выходов последнего слоя требует
применения уравнения (3) к каждому слою от входа сети к ее
выходу.
Обратный проход. Подстройка весов выходного слоя.
Так как для каждого нейрона выходного слоя задано целевое значение,
то подстройка весов легко осуществляется с использованием
дельта-правила. Внутренние слои называют "скрытыми слоями", для их
выходов не имеется целевых значений для сравнения, поэтому обучение
усложняется.
Рассмотрим процесс обучения для одного веса от нейрона 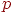 в
скрытом слое в
скрытом слое 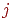 к
нейрону к
нейрону  в выходном слое в выходном слое  .
Выход нейрона слоя .
Выход нейрона слоя  ,
вычитаемый из целевого значения (Target), дает сигнал ошибки. Он
умножается на производную сжимающей функции ,
вычитаемый из целевого значения (Target), дает сигнал ошибки. Он
умножается на производную сжимающей функции ![[OUT(1 - OUT)]](6b2906cd312c87b0b2ca1014df61e958.png) ,
вычисленную для этого нейрона слоя ,
вычисленную для этого нейрона слоя  ,
давая, таким образом, величину ,
давая, таким образом, величину 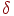 . .
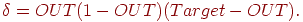 |
(4)
|
Затем 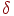 умножается на величину
умножается на величину  нейрона
нейрона 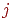 , из которого выходит рассматриваемый вес. Это
произведение, в свою очередь, умножается на коэффициент скорости
обучения , из которого выходит рассматриваемый вес. Это
произведение, в свою очередь, умножается на коэффициент скорости
обучения 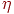 (обычно
от 0,01 до 1,0), и результат прибавляется к весу. Такая же процедура
выполняется для каждого веса от нейрона скрытого слоя к нейрону в
выходном слое. (обычно
от 0,01 до 1,0), и результат прибавляется к весу. Такая же процедура
выполняется для каждого веса от нейрона скрытого слоя к нейрону в
выходном слое.
Следующие уравнения иллюстрируют это вычисление:
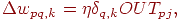 |
(5)
|
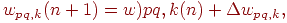 |
(6)
|
где 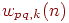 —
величина веса от нейрона —
величина веса от нейрона 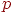 в
скрытом слое в
скрытом слое  к
нейрону к
нейрону  в выходном слое на шаге в выходном слое на шаге  (до коррекции); отметим, что индекс
(до коррекции); отметим, что индекс  относится к слою, в котором заканчивается данный вес (т. е. к слою,
с которым он объединен);
относится к слою, в котором заканчивается данный вес (т. е. к слою,
с которым он объединен); 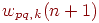 — величина веса на шаге — величина веса на шаге  (после коррекции); (после коррекции); 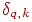 — величина — величина  для нейрона для нейрона  ,
в выходном слое ,
в выходном слое  ; ;
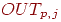 — величина — величина  для нейрона
для нейрона 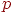 в
скрытом слое в
скрытом слое 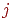 . .
Подстройка весов скрытого слоя. Рассмотрим один нейрон в
скрытом слое, предшествующем выходному слою. При проходе вперед этот
нейрон передает свой выходной сигнал нейронам в выходном слое через
соединяющие их веса. Во время обучения эти веса функционируют в
обратном порядке, пропуская величину 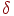 от выходного слоя назад к скрытому слою. Каждый из этих
весов умножается на величину от выходного слоя назад к скрытому слою. Каждый из этих
весов умножается на величину 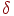 нейрона, к которому он присоединен в выходном слое.
Величина нейрона, к которому он присоединен в выходном слое.
Величина 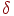 ,
необходимая для нейрона скрытого слоя, получается суммированием всех
таких произведений и умножением на производную сжимающей функции
(см. рис.
4.4): ,
необходимая для нейрона скрытого слоя, получается суммированием всех
таких произведений и умножением на производную сжимающей функции
(см. рис.
4.4):
![\delta_{q,k}=OUT_{p,j}(1-OUT_{p,j})\left[\sum_q\delta_{q,k}
w_{pq,k}\right].
\vspace{-2mm}](1191662b6e4789236276217675af21df.png) |
(7)
|
Когда значение 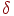 получено, веса, питающие первый скрытый уровень, могут
быть подкорректированы с помощью уравнений (5) и (6), где индексы
модифицируются в соответствии со слоем. получено, веса, питающие первый скрытый уровень, могут
быть подкорректированы с помощью уравнений (5) и (6), где индексы
модифицируются в соответствии со слоем.
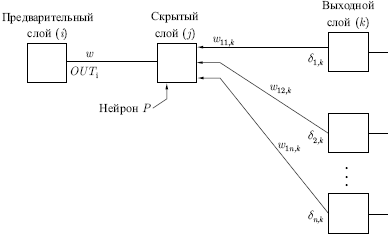
Рис. 4.4.
Для каждого нейрона в данном скрытом слое должно быть вычислено
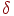 и подстроены все веса, ассоциированные с этим слоем. Этот
процесс повторяется слой за слоем по направлению к входу, пока все
веса не будут подкорректированы. и подстроены все веса, ассоциированные с этим слоем. Этот
процесс повторяется слой за слоем по направлению к входу, пока все
веса не будут подкорректированы.
С помощью векторных обозначений операция обратного
распространения ошибки может быть записана значительно компактнее.
Обозначим множество величин 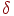 выходного слоя через выходного слоя через  и множество весов выходного слоя как массив
и множество весов выходного слоя как массив 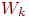 . Чтобы получить . Чтобы получить 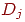 , , 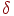 -вектор выходного слоя, достаточно следующих двух
операций: -вектор выходного слоя, достаточно следующих двух
операций:
- Умножить о-вектор выходного слоя
 на транспонированную матрицу весов на транспонированную матрицу весов 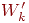 , соединяющую скрытый уровень с выходным уровнем. , соединяющую скрытый уровень с выходным уровнем.
- Умножить каждую компоненту полученного произведения на
производную сжимающей функции соответствующего нейрона в скрытом
слое.
Добавление нейронного смещения. Во многих случаях
желательно наделять каждый нейрон обучаемым смещением. Это позволяет
сдвигать начало отсчета логистической функции, давая эффект,
аналогичный подстройке порога персептронного нейрона, и приводит к
ускорению процесса обучения. Такая возможность может быть легко
введена в обучающий алгоритм с помощью добавляемого к каждому
нейрону веса, который присоединен к  .
Этот вес обучается так же, как и все остальные веса, за исключением
того, что подаваемый на него сигнал всегда равен .
Этот вес обучается так же, как и все остальные веса, за исключением
того, что подаваемый на него сигнал всегда равен  ,
а не выходу нейрона предыдущего слоя. ,
а не выходу нейрона предыдущего слоя.
Импульс. Существует метод ускорения обучения для алгоритма обратного распространения,
увеличивающий также устойчивость процесса. Этот метод, названный
импульсом, заключается в добавлении к коррекции веса члена,
пропорционального величине предыдущего изменения веса. Как только
происходит коррекция, она "запоминается" и служит для модификации
всех последующих коррекций. Уравнения коррекции модифицируются
следующим образом:
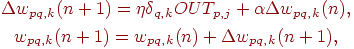
где  —
коэффициент импульса, который обычно устанавливается около 0,9. —
коэффициент импульса, который обычно устанавливается около 0,9.
Используя метод импульса, сеть стремится идти по дну "узких
оврагов" поверхности ошибки (если таковые имеются), а не двигаться
"от склона к склону". Этот метод, по-видимому, хорошо работает на
некоторых задачах, но дает слабый или даже отрицательный эффект на
других.
Существует сходный метод, основанный на экспоненциальном
сглаживании, который может иметь преимущество в ряде
приложений. 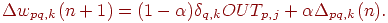
Затем вычисляется изменение веса 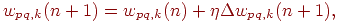
где  —
коэффициент сглаживания, варьируемый в диапазоне от 0,0 до 1,0. Если —
коэффициент сглаживания, варьируемый в диапазоне от 0,0 до 1,0. Если
 равен 1,0, то новая коррекция игнорируется и повторяется
предыдущая. В области между 0 и 1 коррекция веса сглаживается
величиной, пропорциональной равен 1,0, то новая коррекция игнорируется и повторяется
предыдущая. В области между 0 и 1 коррекция веса сглаживается
величиной, пропорциональной  . По-прежнему, . По-прежнему, 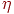 является коэффициентом скорости обучения, служащим для
управления средней величиной изменения веса. является коэффициентом скорости обучения, служащим для
управления средней величиной изменения веса.
Дальнейшие алгоритмические разработки
Многими исследователями были предложены методы улучшения и
обобщения описанного выше основного алгоритма
обратного распространения. Литература в этой области слишком
обширна, чтобы ее можно было здесь охватить. Кроме того, сейчас еще
слишком рано давать окончательные оценки. Некоторые из этих подходов
могут оказаться действительно фундаментальными, другие же со
временем исчезнут. Перечислим некоторые из наиболее многообещающих
разработок.
Метод ускорения сходимости алгоритма
обратного распространения. Названный обратным
распространением второго порядка, он использует вторые производные
для более точной оценки требуемой коррекции весов. Показано, что
этот алгоритм оптимален в том смысле, что невозможно улучшить
оценку, даже используя производные более высокого порядка. Метод
требует дополнительных вычислений по сравнению с обратным
распространением первого порядка, и необходимы дальнейшие
эксперименты для доказательства оправданности этих затрат.
Метод улучшения характеристик обучения сетей
обратного распространения. Указывается, что общепринятый от 0
до 1 динамический диапазон входов и выходов скрытых нейронов
неоптимален. Так как величина коррекции веса 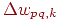 пропорциональна выходному уровню нейрона, порождающего
пропорциональна выходному уровню нейрона, порождающего 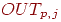 , то нулевой уровень ведет к тому, что вес не меняется. При
двоичных входных векторах половина входов в среднем будет равна
нулю, и веса, с которыми они связаны, не будут обучаться! Решение
состоит в приведении входов к значениям , то нулевой уровень ведет к тому, что вес не меняется. При
двоичных входных векторах половина входов в среднем будет равна
нулю, и веса, с которыми они связаны, не будут обучаться! Решение
состоит в приведении входов к значениям  и добавлении смещения к сжимающей функции, чтобы она также
принимала значения и добавлении смещения к сжимающей функции, чтобы она также
принимала значения  . Новая сжимающая функция выглядит следующим образом: . Новая сжимающая функция выглядит следующим образом:
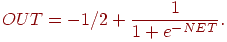
С помощью таких простых средств время сходимости сокращается в
среднем от 30 до 50%. Это один из примеров практической модификации,
существенно улучшающей характеристику алгоритма.
Методика обратного распространения применима и к сетям с
обратными связями, т. е. к таким сетям, у которых выходы подаются
через обратную связь на входы. Как показано, обучение в подобных
системах может быть очень быстрым и критерии устойчивости легко
удовлетворяются.
Применение
Обратное распространение было применено в широкой сфере
прикладных исследований. Некоторые из них описываются здесь, чтобы
продемонстрировать богатые возможности этого метода.
Фирма NEC в Японии объявила недавно, что обратное распространение
было ею использовано для визуального распознавания букв, причем
точность превысила 99%. Это улучшение было достигнуто с помощью
комбинации обычных алгоритмов с сетью обратного
распространения, обеспечивающей дополнительную проверку.
Достигнут впечатляющий успех с Net-Talk системой, которая
превращает печатный английский текст в высококачественную речь.
Магнитофонная запись процесса обучения сильно напоминает звуки
голоса ребенка на разных этапах обучения речи.
Обратное распространение также использовалось в машинном
распознавании рукописных английских слов. Буквы, нормализованные по
размеру, наносились на сетку, и брались проекции линий, пересекающих
квадраты сетки. Эти проекции служили затем входами для сети обратного распространения. Сообщалось о
точности 99,7% при использовании словарного фильтра.
Обратное распространение успешно применяется при сжатии
изображений, когда образы представляются одним битом на пиксель, что
явилось восьмикратным улучшением по сравнению с входными
данными.
|




