Переобучение и обобщение
Одна из наиболее серьезных трудностей алгоритма обратного распределения заключается в
том, что таким образом мы минимизируем не ту ошибку, которую на
самом деле нужно минимизировать, — ошибку, которую можно ожидать от
сети, когда ей будут подаваться совершенно новые наблюдения. Иначе
говоря, мы хотели бы, чтобы нейронная сеть обладала способностью
обобщать результат на новые наблюдения. В действительности,
сеть обучается минимизировать ошибку на обучающем множестве, и в
отсутствие идеального и бесконечно большого обучающего множества это
совсем не то же самое, что минимизировать "настоящую" ошибку на
поверхности ошибок в заранее неизвестной модели явления.
Сильнее всего это различие проявляется в проблеме переобучения, или слишком близкой
подгонки. Это явление проще будет продемонстрировать не для
нейронной сети, а на примере аппроксимации посредством полиномов, —
при этом суть явления абсолютно та же.
Полином (или многочлен) — это выражение, содержащее только
константы и целые степени независимой переменной. Графики полиномов
могут иметь различную форму, причем чем выше степень многочлена (и,
тем самым, чем больше членов в него входит), тем более сложной может
быть эта форма. Если у нас есть некоторые данные, мы можем
попробовать подогнать к ним полиномиальную кривую (модель) и
получить, таким образом, объяснение для имеющейся зависимости. Наши
данные могут быть зашумлены, поэтому нельзя считать, что самая
лучшая модель задается кривой, которая в точности проходит через все
имеющиеся точки. Полином низкого порядка может быть недостаточно
гибким средством для аппроксимации данных, в то время как полином
высокого порядка может оказаться чересчур гибким и будет точно
следовать данным, принимая при этом форму замысловатую и не имеющую
никакого отношения к реальной зависимости.
У нейронной сети проблема точно такая же. Сети с большим числом
весов моделируют более сложные функции и, следовательно, склонны к
переобучению. Сеть же с небольшим числом
весов может оказаться недостаточно гибкой для того, чтобы
смоделировать имеющуюся зависимость. Например, сеть без
промежуточных слоев моделирует обычную линейную функцию.
Как же выбрать "правильную" степень сложности для сети? Почти
всегда более сложная сеть дает меньшую ошибку, но это может
свидетельствовать не о хорошем качестве модели, а о переобучении. Выход состоит в том, чтобы
использовать механизм контрольной кросс-проверки. Мы
резервируем часть обучающих наблюдений и не используем их в обучении
по алгоритму обратного распространения.
Вместо этого, по мере работы алгоритма, они используются для
независимого контроля результата. В самом начале работы ошибка сети
на обучающем и контрольном множестве будет одинаковой (если они
существенно отличаются, то, вероятно, разбиение всех наблюдений на
два множества было неоднородно). По мере того как сеть обучается,
ошибка обучения, естественно, убывает, и, пока обучение уменьшает
действительную функцию ошибок, ошибка на контрольном множестве также
будет убывать. Если же контрольная ошибка перестала убывать или даже
стала расти, значит, сеть начала слишком близко аппроксимировать
данные и обучение следует остановить. Это явление чересчур точной
аппроксимации в процессе обучения и называется переобучением. Если такое случилось, то
обычно советуют уменьшить число скрытых элементов и/или слоев, ибо
сеть является слишком мощной для данной задачи. Если же сеть,
наоборот, была взята недостаточно богатой для того, чтобы
моделировать имеющуюся зависимость, то переобучения, скорее всего, не произойдет и обе
ошибки — обучения и проверки — не достигнут достаточного уровня
малости.
Описанные проблемы с локальными
минимумами и выбором размера сети приводят к тому, что при
практической работе с нейронными сетями, как правило, приходится
экспериментировать с большим числом различных сетей, порой обучая
каждую из них несколько раз (чтобы не быть введенным в заблуждение
локальными минимумами) и сравнивая
полученные результаты. Главным показателем качества результата
является здесь контрольная ошибка. В соответствии с общенаучным
принципом, согласно которому при прочих равных следует предпочесть
более простую модель, имеет смысл из двух сетей с приблизительно
равными ошибками контроля выбрать ту, которая меньше.
Необходимость многократных экспериментов ведет к тому, что
контрольное множество начинает играть ключевую роль в выборе модели,
то есть становится частью процесса обучения. Тем самым ослабляется
его роль как независимого критерия качества модели — при большом
числе экспериментов есть риск выбрать "удачную" сеть, дающую хороший
результат на контрольном множестве. Для того чтобы придать
окончательной модели должную надежность, часто (по крайней мере,
когда объем обучающих данных это позволяет) поступают так:
резервируют еще одно, тестовое множество наблюдений. Итоговая модель
тестируется на данных из этого множества, чтобы убедиться, что
результаты, достигнутые на обучающем и контрольном множествах,
реальны, а не являются артефактами процесса обучения. Разумеется,
для того чтобы соответствовать своей роли, тестовое множество должно
быть использовано только один раз: если его использовать повторно
для корректировки процесса обучения, то оно фактически превратится в
контрольное множество.
Отбор данных
На всех предыдущих этапах мы постоянно опирались на одно
предположение, а именно: обучающее, контрольное и тестовое множества
должны быть репрезентативными (представительными) с точки зрения
существа задачи (более того, эти множества должны быть
репрезентативны каждое в отдельности). Известное изречение
программистов "garbage in, garbage out" ("мусор на входе — мусор на
выходе") нигде не справедливо в такой степени, как при нейросетевом
моделировании. Если обучающие данные не репрезентативны, то модель,
как минимум, будет не очень хорошей, а в худшем случае —
бесполезной. Имеет смысл перечислить ряд причин, которые ухудшают
качество обучающего множества.
Будущее непохоже на прошлое. Обычно в качестве обучающих
берутся исторические данные. Если обстоятельства изменились, то
закономерности, имевшие место в прошлом, могут больше не
действовать.
Следует учесть все возможности. Нейронная сеть может
обучаться только на тех данных, которыми она располагает.
Предположим, что лица с годовым доходом более $100000 имеют высокий
кредитный риск, а обучающее множество не содержало лиц с доходом
более $40000 в год. Тогда едва ли можно ожидать от сети правильного
решения в совершенно новой для нее ситуации.
Сеть обучается тому, чему проще всего обучиться.
Классическим (возможно, вымышленным) примером является система
машинного зрения, предназначенная для автоматического распознавания
танков. Сеть обучалась на ста картинках, содержащих изображения
танков, и на ста других картинках, где танков не было. Был достигнут
стопроцентно "правильный" результат. Но когда на вход сети были
поданы новые данные, она безнадежно провалилась. В чем же была
причина? Выяснилось, что фотографии с танками были сделаны в
пасмурную, дождливую погоду, а фотографии без танков — в солнечный
день. Сеть научилась улавливать (очевидную) разницу в общей
освещенности. Чтобы сеть могла результативно работать, ее следовало
обучать на данных, где присутствовали бы все погодные условия и типы
освещения, при которых сеть будут реально использовать, — и это не
говоря еще о рельефе местности, угле и дистанции съемки и т.д.
Несбалансированный набор данных. Коль скоро сеть
минимизирует общую погрешность, важное значение приобретают
пропорции, в которых представлены данные различных типов. Сеть,
обученная на 900 хороших и 100 плохих примерах, будет искажать
результат в пользу хороших наблюдений, поскольку это позволит
алгоритму уменьшить общую погрешность (которая определяется в
основном хорошими случаями). Если в реальной популяции хорошие и
плохие объекты представлены в другой пропорции, то результаты,
выдаваемые сетью, могут оказаться неверными. Хорошим примером служит
задача выявления заболеваний. Пусть, например, при обычных
обследованиях в среднем 90% человек оказываются здоровыми. Сеть
обучается на имеющихся данных, в которых пропорция здоровые/больные
равна 90/10. Затем она применяется для диагностики пациентов с
определенным жалобами, среди которых это соотношение уже 50/50. В
этом случае сеть будет ставить диагноз чересчур осторожно и не
распознает заболевание у некоторых больных. Если же, наоборот, сеть
обучить на данных "с жалобами", а затем протестировать на "обычных"
данных, то она будет выдавать повышенное число неправильных
диагнозов о наличии заболевания. В таких ситуациях обучающие данные
нужно скорректировать так, чтобы были учтены различия в
распределении (например, можно повторять редкие наблюдения или
удалить часто встречающиеся), или же видоизменить решения,
выдаваемые сетью, посредством матрицы потерь. Как правило,
лучше всего постараться равномерно представить наблюдения различных
типов и соответственно этому интерпретировать результаты, которые
выдает сеть.
Как обучается многослойный персептрон
Мы сможем лучше понять, как устроен и как обучается многослойный
персептрон, если выясним, какие функции он способен моделировать.
Вспомним, что уровнем активации элемента называется взвешенная сумма
его входов с добавленным к ней пороговым значением. Таким образом,
уровень активации представляет собой простую линейную функцию
входов. Эта активация затем преобразуется с помощью сигмоидной
(имеющей S- образную форму) кривой.
Комбинация линейной функции нескольких переменных и скалярной
сигмовидной функции приводит к характерному профилю "сигмовидного
склона", который выдает элемент первого промежуточного слоя. На рис.
5.1 соответствующая поверхность изображена в виде функции двух
входных переменных. Элемент с большим числом входов выдает
многомерный аналог такой поверхности. При изменении весов и порогов
меняется и поверхность отклика; может меняться как ориентация всей
поверхности, так и крутизна склона — большим значениям весов
соответствует более крутой склон. Так, например, если увеличить все
веса в два раза, то ориентация не изменится, а наклон будет более
крутым. В многослойной сети подобные функции отклика комбинируются
друг с другом с помощью последовательного взятия их линейных
комбинаций и применения нелинейных функций активации. На рис.
5.2 изображена типичная поверхность отклика для сети с одним
промежуточным слоем, состоящим из двух элементов, и одним выходным
элементом, для классической задачи "исключающего или". Две разных
сигмоидных поверхности объединены в одну поверхность, имеющую форму
буквы "U".
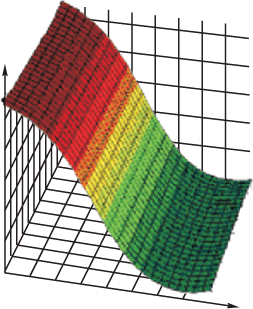
Рис. 5.1.
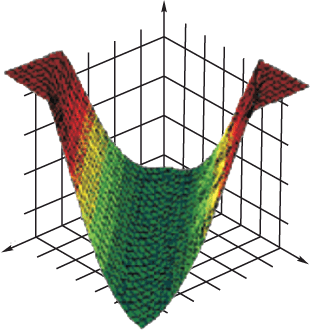
Рис. 5.2.
Перед началом обучения сети весам и порогам случайным образом
присваиваются небольшие по величине начальные значения. Тем самым,
отклики отдельных элементов сети имеют малый наклон и ориентированы
хаотично — фактически они не связаны друг с другом. По мере того,
как происходит обучение, поверхности отклика элементов сети
вращаются и сдвигаются в нужное положение, а значения весов
увеличиваются, поскольку они должны моделировать отдельные участки
целевой поверхности отклика.
В задачах классификации выходной элемент должен выдавать сильный
сигнал в случае, если данное наблюдение принадлежит к интересующему
нас классу, и слабый — в противоположном случае. Иначе говоря, этот
элемент должен стремиться смоделировать функцию, равную единице в
области пространства объектов, где располагаются объекты из нужного
класса, и равную нулю вне этой области. Такая конструкция известна
как дискриминантная функция в задачах распознавания.
"Идеальная" дискриминантная функция должна иметь плоскую структуру:
точки соответствующей поверхности будут располагаться либо на
нулевом уровне, либо на высоте "единица".
Если сеть не содержит скрытых элементов, то на выходе она может
моделировать только одинарный "сигмовидный склон": точки,
находящиеся по одну его сторону, располагаются низко, по другую —
высоко. При этом всегда будет существовать область между ними (на
склоне), где высота принимает промежуточные значения, но по мере
увеличения весов эта область будет сужаться.
Такой сигмовидный склон фактически работает как линейная
дискриминантная функция. Точки, лежащие по одну сторону склона,
классифицируются как принадлежащие нужному классу, а лежащие по
другую сторону — как не принадлежащие. Следовательно, сеть без
скрытых слоев может служить классификатором только в
линейно-отделимых задачах: когда можно провести линию (или, в случае
более высоких размерностей, гиперплоскость), разделяющую точки в
пространстве признаков.
Сеть, содержащая один промежуточный слой, строит несколько
сигмоидных склонов, — по одному для каждого скрытого элемента, — и
затем выходной элемент комбинирует из них "возвышенность". Эта
возвышенность получается выпуклой, т.е. не содержащей впадин. При
этом в некоторых направлениях она может уходить на бесконечность
(как длинный полуостров). Подобная сеть может моделировать
большинство реальных задач классификации.
Сеть с двумя промежуточными слоями строит комбинацию из
нескольких таких возвышенностей. Их будет столько, сколько элементов
во втором слое, и у каждой из них будет столько сторон, сколько
элементов было в первом скрытом слое. После несложного размышления
делаем вывод, что, используя достаточное число таких возвышенностей,
можно воспроизвести поверхность любой формы — в том числе с
впадинами и вогнутостями.
Как следствие наших рассмотрений мы получаем, что, теоретически,
для моделирования любой задачи достаточно многослойного персептрона
с двумя промежуточными слоями (в точной формулировке этот результат
известен как теорема Колмогорова). При этом может оказаться, что для
решения некоторой конкретной задачи будет более простой и удобной
сеть с еще большим числом слоев. Однако для решения большинства
практических задач достаточно всего одного промежуточного слоя, два
слоя применяются как резерв в особых случаях, а сети с тремя слоями
практически не применяются.
В задачах классификации очень важно понять, как следует
интерпретировать те точки, которые попали на склон или лежат близко
от него. Стандартный подход заключается в том, чтобы для пороговых
значений установить некоторые доверительные пределы (принятия или
отвержения), которые должны быть достигнуты, чтобы данный элемент
считался "принявшим решение". Например, если установлены пороги
принятия/отвержения 0,95/0.05, то при уровне выходного сигнала выше
0,95 элемент считается активным, при уровне ниже 0,05 — неактивным,
а в промежутке — "неопределенным". Имеется и более тонкий (и,
вероятно, более полезный) способ интерпретировать уровни выходного
сигнала: считать их вероятностями. В этом случае сеть выдает
несколько большую информацию, чем просто "да/нет": она сообщает нам,
насколько (в некотором формальном смысле) мы можем доверять ее
решению. При этом, однако, вероятностная интерпретация обоснована
только в том случае, если выполняются определенные предположения о
распределении исходных данных (конкретно, что данные являются
выборкой из некоторого распределения, принадлежащего к семейству
экспоненциальных распределений). Здесь, как и ранее, может быть
принято решение по классификации, но, кроме того, вероятностная
интерпретация позволяет ввести концепцию "решения с минимальными
затратами".
Предостережения
Несмотря на многочисленные успешные применения обратного
распространения, оно не является панацеей. Больше всего
неприятностей доставляет неопределенно долгий процесс обучения. В
сложных задачах для обучения сети могут потребоваться дни или даже
недели, она может и вообще не обучиться. Длительное время обучения
может быть результатом неоптимального выбора длины шага. Неудачи в
обучении обычно возникают по двум причинам: паралича сети и попадания в локальный минимум.
Паралич сети
В процессе обучения сети значения весов могут в результате
коррекции стать очень большими величинами. Это может привести к
тому, что все или большинство нейронов будут функционировать при
очень больших значениях OUT, в области, где производная сжимающей
функции очень мала. Так как посылаемая обратно в процессе обучения
ошибка пропорциональна этой производной, то процесс обучения может
практически замереть. Теоретически эта проблема изучена плохо.
Обычно пытаются уменьшать размера шага
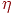 , но это увеличивает время обучения. Различные эвристики
использовались для предохранения от паралича или для восстановления после него, но
пока что они могут рассматриваться лишь как экспериментальные. , но это увеличивает время обучения. Различные эвристики
использовались для предохранения от паралича или для восстановления после него, но
пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы
В прошлой лекции было описано, как с помощью алгоритма обратного распространения
осуществляется градиентный спуск по поверхности ошибок. Короче
говоря, происходит следующее: в данной точке поверхности находится
направление скорейшего спуска, затем делается прыжок вниз на
расстояние, пропорциональное коэффициенту скорости обучения и
крутизне склона, при этом учитывается инерция, то есть стремление
сохранить прежнее направление движения. Можно сказать, что метод
ведет себя как слепой кенгуру — каждый раз прыгает в направлении,
которое кажется ему наилучшим. На самом деле, шаг спуска вычисляется
отдельно для всех обучающих наблюдений, взятых в случайном порядке,
но в результате получается достаточно хорошая аппроксимация спуска
по совокупной поверхности ошибок. Существуют и другие алгоритмы
обучения, однако все они используют ту или иную стратегию скорейшего
продвижения к точке минимума.
Обратное распространение использует разновидность градиентного
спуска, т. е. осуществляет спуск вниз по поверхности ошибки,
непрерывно подстраивая веса в направлении к минимуму. Поверхность
ошибки сложной сети сильно изрезана и состоит из холмов, долин,
складок и оврагов в пространстве высокой размерности. Сеть может
попасть в локальный минимум (неглубокую
долину), когда рядом имеется гораздо более глубокий минимум. В точке
локального минимума все направления ведут
вверх и сеть неспособна из него выбраться. Статистические методы
обучения могут помочь избежать этой ловушки, но они медленны.
П.Д.Вассерман предложил метод, объединяющий статистические методы
машины Коши с градиентным спуском обратного распространения и
приводящий к системе, которая находит глобальный минимум, сохраняя
высокую скорость обратного распространения. Это будет обсуждаться в
следующих лекциях.
Размер шага
Внимательный разбор доказательства сходимости показывает, что
коррекции весов предполагаются бесконечно малыми. Ясно, что это
неосуществимо на практике, так как ведет к бесконечному времени
обучения. Размер шага должен браться
конечным, и при определении его приходится полагаться только на
опыт. Если размер шага очень мал, то
сходимость слишком медленная, если же очень велик, то может
возникнуть паралич или постоянная
неустойчивость. П.Д.Вассерман описал адаптивный алгоритм выбора
шага, автоматически корректирующий размер
шага в процессе обучения.
Временная неустойчивость
Если сеть учится распознавать буквы, то нет смысла учить "Б",
если при этом забывается "А". Процесс обучения должен быть таким,
чтобы сеть обучалась на всем обучающем множестве без пропусков того,
что уже выучено. В доказательстве сходимости это условие выполнено,
но требуется также, чтобы сети предъявлялись все векторы обучающего
множества, прежде чем выполняется коррекция весов. Необходимые
изменения весов должны вычисляться на всем множестве, что требует
дополнительной памяти; после ряда таких обучающих циклов веса
сойдутся к минимальной ошибке. Этот метод может оказаться
бесполезным, если сеть находится в постоянно меняющейся внешней
среде, так что второй раз один и тот же вектор может уже не
повториться. В этом случае процесс обучения может никогда не
сойтись, бесцельно блуждая или сильно осциллируя. В этом смысле
обратное распространение не похоже на биологические системы. Как
будет указано на следующих лекциях, это несоответствие (среди
прочих) привело к системе ART, принадлежащей Гроссбергу.
|




