|
Стохастические методы полезны как для
обучения искусственных нейронных сетей, так и для получения выхода
от уже обученной сети. Стохастические методы
обучения приносят большую пользу, позволяя исключать
локальные минимумы в процессе обучения. Но с ними также связан ряд
проблем.
Использование обучения
Искусственная нейронная сеть обучается с помощью некоторого
процесса, модифицирующего ее веса. Если обучение успешно, то
предъявление сети множества входных сигналов приводит к появлению
желаемого множества выходных сигналов. Имеется два класса обучающих
методов: детерминистский и стохастический.
Детерминистский метод обучения шаг за шагом осуществляет
процедуру коррекции весов сети, основанную на использовании их
текущих значений, а также величин входов, фактических выходов и
желаемых выходов. Обучение персептрона является примером подобного
детерминистского метода.
Стохастические методы обучения
выполняют псевдослучайные изменения величин весов, сохраняя те
изменения, которые ведут к улучшениям. Чтобы показать это наглядно,
рассмотрим рис.
7.1, на котором изображена типичная сеть, где нейроны соединены
с помощью весов. Выход нейрона является здесь взвешенной суммой его
входов, которая преобразована с помощью нелинейной функции. Для
обучения сети могут быть использованы следующие процедуры:
- Выбрать вес случайным образом и подкорректировать его на
небольшое случайное число. Предъявить множество входов и вычислить
получающиеся выходы.
- Сравнить эти выходы с желаемыми выходами и вычислить величину
разности между ними. Общепринятый метод состоит в нахождении
разности между фактическим и желаемым выходами для каждого
элемента обучаемой пары, возведение разностей в квадрат и
нахождение суммы этих квадратов. Целью обучения является
минимизация этой разности, часто называемой целевой
функцией.
- Выбрать вес случайным образом и подкорректировать его на
небольшое случайное значение. Если коррекция помогает (уменьшает
целевую функцию), то сохранить ее, в противном случае вернуться к
первоначальному значению веса.
- Повторять шаги с 1 по 3 до тех пор, пока сеть не будет обучена
в достаточной степени.
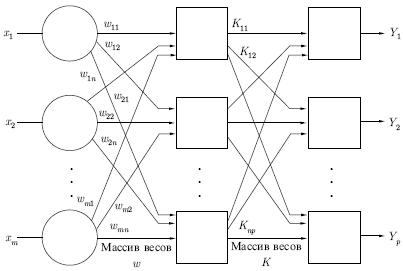
Рис. 7.1.
Этот процесс стремится минимизировать целевую функцию, но может
попасть, как в ловушку, в неудачное решение. На рис.
7.2 показано, как это может происходить в системе с единственным
весом. Допустим, что первоначально вес взят равным значению в точке
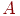 .
Если случайные шаги по весу малы, то любые отклонения от точки .
Если случайные шаги по весу малы, то любые отклонения от точки 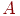 увеличивают целевую функцию и будут отвергнуты. Лучшее значение
веса, принимаемое в точке
увеличивают целевую функцию и будут отвергнуты. Лучшее значение
веса, принимаемое в точке  ,
никогда не будет найдено, и система будет поймана в ловушку
локальным минимумом вместо глобального минимума в точке ,
никогда не будет найдено, и система будет поймана в ловушку
локальным минимумом вместо глобального минимума в точке  .
Если же случайные коррекции веса очень велики, то как точка .
Если же случайные коррекции веса очень велики, то как точка 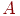 ,
так и точка ,
так и точка  будут часто посещаться, но то же самое будет верно и для каждой
другой точки. Вес будет меняться так резко, что он никогда не
установится в желаемом минимуме.
будут часто посещаться, но то же самое будет верно и для каждой
другой точки. Вес будет меняться так резко, что он никогда не
установится в желаемом минимуме.
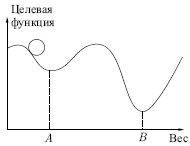
Рис. 7.2.
Полезная стратегия для избежания подобных проблем состоит в
больших начальных шагах и постепенном уменьшении размера среднего
случайного шага. Это позволяет сети вырываться из локальных
минимумов и в то же время гарантирует окончательную стабилизацию
сети.
Ловушки локальных минимумов досаждают всем алгоритмам обучения,
основанным на поиске минимума (включая персептрон и сети обратного
распространения), и представляют серьезную и широко распространенную
трудность, которую почему-то часто игнорируют. Стохастические методы позволяют решить эту
проблему. Стратегия коррекции весов, вынуждающая веса принимать
значение глобального оптимума в точке  ,
вполне возможна. ,
вполне возможна.
В качестве объясняющей аналогии предположим, что на рис.
7.2 изображен шарик на поверхности внутри коробки. Если коробку
сильно потрясти в горизонтальном направлении, то шарик будет быстро
перекатываться от одного края к другому. Нигде не задерживаясь, в
каждый момент времени шарик будет с равной вероятностью находиться в
любой точке поверхности.
Если постепенно уменьшать силу встряхивания, то будет достигнуто
условие, при котором шарик будет на короткое время "застревать" в
точке  . При еще более слабом встряхивании шарик будет на короткое
время останавливаться как в точке . При еще более слабом встряхивании шарик будет на короткое
время останавливаться как в точке 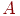 ,
так и в точке ,
так и в точке  .
При непрерывном уменьшении силы встряхивания будет достигнута
критическая точка, когда сила встряхивания достаточна для
перемещения шарика из точки .
При непрерывном уменьшении силы встряхивания будет достигнута
критическая точка, когда сила встряхивания достаточна для
перемещения шарика из точки 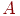 в
точку в
точку  , но недостаточна для того, чтобы шарик мог "вскарабкаться"
из , но недостаточна для того, чтобы шарик мог "вскарабкаться"
из  в в 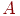 .
Таким образом, окончательно шарик остановится в точке глобального
минимума, когда амплитуда встряхивания уменьшится до нуля. .
Таким образом, окончательно шарик остановится в точке глобального
минимума, когда амплитуда встряхивания уменьшится до нуля.
Искусственные нейронные сети могут обучаться, по существу, тем же
способом при помощи случайной коррекции весов. Вначале делаются
большие случайные коррекции с сохранением только тех изменений
весов, которые уменьшают целевую функцию. Затем средний размер шага
постепенно уменьшается, и глобальный минимум в конце концов
достигается.
Эта процедура весьма напоминает отжиг
металла, поэтому для ее описания часто используют термин
"имитация отжига". В металле, который нагрет до температуры,
превышающей его точку плавления, атомы находятся в сильном
беспорядочном движении. Как и во всех физических системах, атомы
стремятся к состоянию минимума энергии (единому кристаллу, в данном
случае), но при высоких температурах энергия атомных движений
препятствует этому. В процессе постепенного охлаждения металла
возникают все более низкоэнергетические состояния, пока, в конце
концов, не будет достигнуто самое малое из возможных состояний,
глобальный минимум. В процессе отжига распределение
энергетических уровней описывается следующим соотношением: 
где 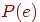 —
вероятность того, что система находится в состоянии с энергией —
вероятность того, что система находится в состоянии с энергией 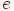 ; ;
 —
постоянная Больцмана; —
постоянная Больцмана;  —
температура по шкале Кельвина. —
температура по шкале Кельвина.
При высоких температурах 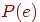 приближается к единице для всех энергетических состояний.
Таким образом, высокоэнергетическое состояние почти столь же
вероятно, как и низкоэнергетическое. По мере уменьшения температуры
вероятность высокоэнергетических состояний уменьшается по отношению
к низкоэнергетическим. При приближении температуры к нулю становится
весьма маловероятным, чтобы система находилась в
высокоэнергетическом состоянии. приближается к единице для всех энергетических состояний.
Таким образом, высокоэнергетическое состояние почти столь же
вероятно, как и низкоэнергетическое. По мере уменьшения температуры
вероятность высокоэнергетических состояний уменьшается по отношению
к низкоэнергетическим. При приближении температуры к нулю становится
весьма маловероятным, чтобы система находилась в
высокоэнергетическом состоянии.
Больцмановское обучение
Этот стохастический метод
непосредственно применим к обучению искусственных нейронных
сетей:
- Определить переменную
 , представляющую искусственную температуру. Придать , представляющую искусственную температуру. Придать  большое начальное значение.
большое начальное значение.
- Предъявить сети множество входов и вычислить выходы и целевую
функцию.
- Дать случайное изменение весу и пересчитать выход сети и
изменение целевой функции в соответствии со сделанным изменением
веса.
- Если целевая функция уменьшилась (улучшилась), то сохранить
изменение веса.
Если изменение веса приводит к увеличению целевой функции, то
вероятность сохранения этого изменения вычисляется с помощью
распределения Больцмана: 
где  —
вероятность изменения —
вероятность изменения  в
целевой функции; в
целевой функции;  —
константа, аналогичная константе Больцмана, выбираемая в зависимости
от задачи; —
константа, аналогичная константе Больцмана, выбираемая в зависимости
от задачи;  —
искусственная температура. —
искусственная температура.
Выбирается случайное число  из равномерного распределения от нуля до единицы. Если
из равномерного распределения от нуля до единицы. Если  больше, чем больше, чем  ,
то изменение сохраняется, в противном случае величина веса
возвращается к предыдущему значению. Это позволяет системе делать
случайный шаг в направлении, портящем целевую функцию, и дает ей тем
самым возможность вырываться из локальных минимумов, где любой малый
шаг увеличивает целевую функцию. ,
то изменение сохраняется, в противном случае величина веса
возвращается к предыдущему значению. Это позволяет системе делать
случайный шаг в направлении, портящем целевую функцию, и дает ей тем
самым возможность вырываться из локальных минимумов, где любой малый
шаг увеличивает целевую функцию.
Для завершения больцмановского
обучения повторяют шаги 3 и 4 для каждого из весов
сети, постепенно уменьшая температуру  ,
пока не будет достигнуто допустимо низкое значение целевой функции.
В этот момент предъявляется другой входной вектор, и процесс
обучения повторяется. Сеть обучается на всех векторах обучающего
множества, с возможным повторением, пока целевая функция не станет
допустимой для всех них. ,
пока не будет достигнуто допустимо низкое значение целевой функции.
В этот момент предъявляется другой входной вектор, и процесс
обучения повторяется. Сеть обучается на всех векторах обучающего
множества, с возможным повторением, пока целевая функция не станет
допустимой для всех них.
Величина случайного изменения веса на шаге 3 может определяться
различными способами. Например, подобно тепловой системе, весовое
изменение  может выбираться в соответствии с гауссовским
распределением: может выбираться в соответствии с гауссовским
распределением:
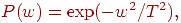
где  —
вероятность изменения веса на величину —
вероятность изменения веса на величину  , ,
 —
искусственная температура. —
искусственная температура.
Так как требуется величина изменения веса  , а не вероятность изменения веса, имеющего величину , а не вероятность изменения веса, имеющего величину  ,
то метод Монте-Карло может быть использован следующим образом: ,
то метод Монте-Карло может быть использован следующим образом:
- Найти кумулятивную вероятность, соответствующую
 . Это есть интеграл от . Это есть интеграл от  в пределах от 0 до в пределах от 0 до  . Поскольку в данном случае . Поскольку в данном случае  не может быть проинтегрирована аналитически, она должна
интегрироваться численно, а результат необходимо затабулировать. не может быть проинтегрирована аналитически, она должна
интегрироваться численно, а результат необходимо затабулировать.
- Выбрать случайное число из равномерного распределения на
интервале (0,1). Используя эту величину в качестве значения
 , найти в таблице соответствующее значение для величины
изменения веса. , найти в таблице соответствующее значение для величины
изменения веса.
Свойства машины Больцмана широко изучены. Скорость уменьшения
температуры должна быть обратно пропорциональна логарифму времени,
чтобы была достигнута сходимость к глобальному минимуму. Скорость
охлаждения в такой системе выражается следующим образом:
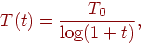
где 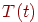 —
искусственная температура как функция времени; —
искусственная температура как функция времени; 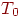 — начальная искусственная температура;
— начальная искусственная температура; 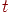 —
искусственное время. —
искусственное время.
Этот разочаровывающий результат предсказывает очень медленную
скорость охлаждения (и вычислений). Вывод подтвержден и
экспериментально. Машины Больцмана часто требуют для обучения очень
большого ресурса времени.
Обучение Коши
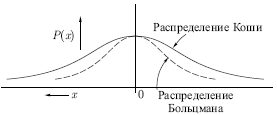
Рис. 7.3.
В этом методе при вычислении величины шага распределение
Больцмана заменяется на распределение
Коши. Распределение Коши имеет,
как показано на рис.
7.3, более длинные "хвосты", увеличивая тем самым вероятность
больших шагов. В действительности, распределение
Коши имеет бесконечную (неопределенную) дисперсию. С помощью
такого простого изменения максимальная скорость уменьшения
температуры становится обратно пропорциональной линейной величине, а
не логарифму, как для алгоритма обучения Больцмана. Это резко
уменьшает время обучения. Зависимость может быть выражена следующим
образом:
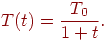
Распределение Коши имеет вид
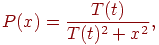
где 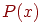 есть
вероятность шага величины есть
вероятность шага величины  . .
В данном уравнении 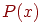 может быть проинтегрирована стандартными методами. Решая
относительно может быть проинтегрирована стандартными методами. Решая
относительно  ,
получаем ,
получаем 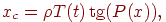
где 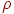 —
коэффициент скорости обучения; —
коэффициент скорости обучения; 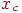 — изменение веса.
— изменение веса.
Теперь применение метода Монте-Карло становится очень простым.
Для нахождения x в этом случае выбирается случайное число из
равномерного распределения на открытом интервале 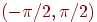 (необходимо ограничить функцию тангенса). Оно подставляется в
формулу (5.7) в качестве
(необходимо ограничить функцию тангенса). Оно подставляется в
формулу (5.7) в качестве 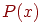 , и с помощью текущей температуры вычисляется величина
шага. , и с помощью текущей температуры вычисляется величина
шага.
Метод искусственной теплоемкости
Несмотря на улучшение, достигаемое с помощью метода Коши, время
обучения может оказаться все еще слишком большим. Для дальнейшего
ускорения этого процесса может быть использован способ, уходящий
своими корнями в термодинамику. В этом методе скорость уменьшения
температуры изменяется в соответствии с искусственной "теплоемкостью", вычисляемой в
процессе обучения.
Во время отжига металла происходят
фазовые переходы, связанные с дискретными изменениями уровней
энергии. При каждом фазовом переходе может происходить резкое
изменение величины, называемой теплоемкостью. Теплоемкость
определяется как скорость изменения температуры в зависимости от
изменения энергии. Изменения теплоемкости происходят из-за попадания
системы в локальные энергетические минимумы.
Искусственные нейронные сети проходят аналогичные фазы в процессе
обучения. На границе фазового перехода искусственная теплоемкость может скачкообразно
измениться. Эта псевдотеплоемкость определяется как средняя скорость
изменения температуры с целевой функцией. В примере шарика в
коробке, приведенном выше, сильная начальная встряска делает среднюю
величину целевой функции фактически не зависящей от малых изменений
температуры, т. е. теплоемкость близка к константе.
Аналогично, при очень низких температурах система замерзает в точке
минимума, так что теплоемкость снова близка к константе.
Ясно, что в каждой из этих областей допустимы сильные изменения
температуры, так как не происходит улучшения целевой функции.
При критической температуре небольшое уменьшение ее значения
приводит к большому изменению средней величины целевой функции.
Возвращаясь к аналогии с шариком, при "температуре", когда шарик
обладает достаточной средней энергией, чтобы перейти из 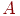 в в
 ,
но не достаточной для перехода из ,
но не достаточной для перехода из  в в
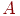 ,
средняя величина целевой функции испытывает скачкообразное
изменение. В этих критических точках алгоритм должен изменять
температуру очень медленно, чтобы гарантировать, что система не
"замерзнет" случайно в точке ,
средняя величина целевой функции испытывает скачкообразное
изменение. В этих критических точках алгоритм должен изменять
температуру очень медленно, чтобы гарантировать, что система не
"замерзнет" случайно в точке 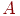 ,
оказавшись пойманной в локальный минимум. Критическая температура
может быть обнаружена по резкому уменьшению искусственной теплоемкости, т.е. средней
скорости изменения температуры с целевой функцией. При достижении
критической температуры скорость изменения температуры должна
замедляться, чтобы гарантировать сходимость к глобальному минимуму.
При всех остальных температурах может без риска использоваться более
высокая скорость снижения температуры, что приводит к значительному
снижению времени обучения. ,
оказавшись пойманной в локальный минимум. Критическая температура
может быть обнаружена по резкому уменьшению искусственной теплоемкости, т.е. средней
скорости изменения температуры с целевой функцией. При достижении
критической температуры скорость изменения температуры должна
замедляться, чтобы гарантировать сходимость к глобальному минимуму.
При всех остальных температурах может без риска использоваться более
высокая скорость снижения температуры, что приводит к значительному
снижению времени обучения.
Обратное распространение и обучение Коши
Обратное распространение обладает преимуществом прямого поиска,
т.е. веса всегда корректируются в направлении, минимизирующем
функцию ошибки. Хотя время обучения и велико, оно существенно
меньше, чем при случайном поиске, выполняемом машиной Коши, когда
отыскивается глобальный минимум, но многие шаги выполняются в
неверном направлении и "съедают" много времени.
Соединение этих двух методов дало хорошие результаты. Коррекция
весов, равная сумме, вычисленной алгоритмом обратного
распространения, и случайный шаг, задаваемый алгоритмом Коши,
приводят к системе, которая сходится и находит глобальный минимум
быстрее, чем система, обучаемая каждым из методов в отдельности.
Простая эвристика используется для избежания паралича сети, который
может возникнуть как при обратном распространении, так и при
обучении по методу Коши.
Трудности, связанные с обратным распространением
Несмотря на богатые возможности, продемонстрированные методом
обратного распространения, при его применении возникает ряд
трудностей, часть из которых, однако, облегчается благодаря
использованию нового алгоритма.
Сходимость. Д.Е.Румелхарт доказал сходимость на языке
дифференциальных уравнений в частных производных. Таким образом,
доказательство справедливо лишь в том случае, когда коррекция весов
выполняется с помощью бесконечно малых шагов. Это условие ведет к
бесконечному времени сходимости, и тем самым метод теряет силу в
практических применениях. В действительности нет доказательства, что
обратное распространение будет сходиться при конечном размере шага.
Эксперименты показывают, что сети обычно обучаются, но время
обучения велико и непредсказуемо.
Локальные минимумы. В обратном распространении для
коррекции весов сети используется градиентный спуск, продвигающийся
к минимуму в соответствии с локальным наклоном поверхности ошибки.
Он хорошо работает в случае сильно изрезанных невыпуклых
поверхностей, которые встречаются в практических задачах. В одних
случаях локальный минимум является приемлемым решением, в других
случаях он неприемлем.
Даже после того как сеть обучена, невозможно сказать, найден ли с
помощью обратного распространения глобальный минимум. Если решение
неудовлетворительно, приходится давать весам новые начальные
случайные значения и повторно обучать сеть без гарантии, что
обучение закончится на этой попытке или что глобальный минимум
вообще будет когда-либо найден.
Паралич. При некоторых условиях сеть может при обучении
попасть в такое состояние, когда модификация весов не ведет к
действительным изменениям сети. Такой "паралич сети" является
серьезной проблемой: один раз возникнув, он может увеличить время
обучения на несколько порядков.
Паралич возникает, когда значительная часть нейронов получает
веса достаточно большие, чтобы дать большие значения NET. В результате величина OUT приближается к своему предельному
значению, а производная от сжимающей функции приближается к нулю.
Как мы видели, алгоритм обратного распространения при вычислении
величины изменения веса использует эту производную в формуле в
качестве коэффициента. Для пораженных параличом нейронов близость
производной к нулю приводит к тому, что изменение веса становится
близким к нулю.
Если подобные условия возникают во многих нейронах сети, то
обучение может замедлиться до почти полной остановки.
Нет теории, способной предсказывать, будет ли сеть парализована
во время обучения или нет. Экспериментально установлено, что малые
размеры шага реже приводят к параличу, но шаг, малый для одной
задачи, может оказаться большим для другой. Цена же паралича может
быть высокой. При моделировании многие часы машинного времени могут
уйти на то, чтобы выйти из паралича.
Трудности с алгоритмом обучения Коши
Несмотря на улучшение скорости обучения, даваемое машиной Коши по
сравнению с машиной Больцмана, время сходимости все еще может в 100
раз превышать время для алгоритма обратного распространения.
Отметим, что сетевой паралич особенно опасен для алгоритма
обучения Коши, в особенности для сети с
нелинейностью типа логистической функции. Бесконечная дисперсия
распределения Коши приводит к изменениям
весов до неограниченных величин. Далее, большие изменения весов
будут иногда приниматься даже в тех случаях, когда они
неблагоприятны, часто приводя к сильному насыщению сетевых нейронов
с вытекающим отсюда риском паралича.
Комбинирование обратного распространения с shape обучением Коши. Коррекция весов в
комбинированном алгоритме, использующем обратное распространение и
обучение Коши, состоит из двух компонент:
(1) направленной компоненты, вычисляемой с использованием алгоритма
обратного распространения, и (2) случайной компоненты, определяемой
распределением Коши. Эти компоненты
вычисляются для каждого веса, и их сумма является величиной, на
которую изменяется вес. Как и в алгоритме Коши, после
вычисления изменения веса вычисляется целевая функция. Если
происходит улучшение, изменение сохраняется безусловно. В противном
случае, оно сохраняется с вероятностью, определяемой распределением
Больцмана. Коррекция веса вычисляется с использованием
представленных ранее уравнений для каждого из алгоритмов: ![w_{mn,k}(n+1) =w_{mn,k}(n) +
\eta [\alpha \Delta w_{mn,k}(n) + (1 - \alpha) \delta_{n,k} OUT_{m,j}]
+ (1 - \eta) x_c,](2ef5768006acfffe83a654d391c9effa.png)
где 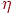 —
коэффициент, управляющий относительными величинами Коши и обратного
распространения в компонентах весового шага. Если ? приравнивается
нулю, система становится полностью машиной Коши. Если ?
приравнивается единице, система становится машиной обратного
распространения. Изменение лишь одного весового коэффициента между
вычислениями весовой функции неэффективно. Оказалось, что лучше
сразу изменять все веса целого слоя, хотя для некоторых задач может
стать выгоднее иная стратегия. Преодоление сетевого паралича
комбинированным методом обучения. Как и в машине Коши, если
изменение веса ухудшает целевую функцию, — с помощью распределения
Больцмана решается, сохранить ли новое значение веса или
восстановить предыдущее значение. Таким образом, имеется конечная
вероятность того, что ухудшающее множество приращений весов будет
сохранено. Так как распределение Коши
имеет бесконечную дисперсию (диапазон изменения тангенса
простирается от —
коэффициент, управляющий относительными величинами Коши и обратного
распространения в компонентах весового шага. Если ? приравнивается
нулю, система становится полностью машиной Коши. Если ?
приравнивается единице, система становится машиной обратного
распространения. Изменение лишь одного весового коэффициента между
вычислениями весовой функции неэффективно. Оказалось, что лучше
сразу изменять все веса целого слоя, хотя для некоторых задач может
стать выгоднее иная стратегия. Преодоление сетевого паралича
комбинированным методом обучения. Как и в машине Коши, если
изменение веса ухудшает целевую функцию, — с помощью распределения
Больцмана решается, сохранить ли новое значение веса или
восстановить предыдущее значение. Таким образом, имеется конечная
вероятность того, что ухудшающее множество приращений весов будет
сохранено. Так как распределение Коши
имеет бесконечную дисперсию (диапазон изменения тангенса
простирается от  до до  на области определения), то весьма вероятно возникновение
больших приращений весов, часто приводящих к сетевому параличу. на области определения), то весьма вероятно возникновение
больших приращений весов, часто приводящих к сетевому параличу.
Очевидное решение, состоящее в ограничении диапазона изменения
весовых шагов, ставит вопрос о математической корректности
полученного таким образом алгоритма. На сегодняшний день доказана
сходимость системы к глобальному минимуму лишь для исходного
алгоритма. Подобного доказательства при искусственном ограничении
размера шага не существует. В действительности экспериментально
выявлены случаи, когда для реализации некоторой функции требуются
большие веса и два больших веса, вычитаясь, дают малую разность.
Другое решение состоит в рандомизации весов тех нейронов, которые
оказались в состоянии насыщения. Его недостаток в том, что оно может
серьезно нарушить обучающий процесс, иногда затягивая его до
бесконечности.
Для решения проблемы паралича был найден метод, не нарушающий
достигнутого обучения. Насыщенные нейроны выявляются с помощью
измерения их сигналов OUT. Когда величина OUT приближается к своему предельному
значению, положительному или отрицательному, на веса, питающие этот
нейрон, действует сжимающая функция. Она подобна используемой для
получения нейронного сигнала OUT, за исключением того, что
диапазоном ее изменения является интервал 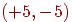 или другое подходящее множество. Тогда модифицированные
весовые значения равны или другое подходящее множество. Тогда модифицированные
весовые значения равны

Эта функция заметно уменьшает величину очень больших весов,
воздействие на малые веса значительно более слабое. Далее, она
поддерживает симметрию, сохраняя небольшие различия между большими
весами. Экспериментально было показано, что эта функция выводит
нейроны из состояния насыщения без нарушения достигнутого в сети
обучения. Не было затрачено серьезных усилий для оптимизации
используемой функции, и другие значения констант могут оказаться
лучшими.
Экспериментальные результаты
Комбинированный алгоритм, использующий обратное распространение и
обучение Коши, применялся для обучения
нескольких больших сетей. Например, этим методом была успешно
обучена система, распознающая рукописные китайские иероглифы. Все же
время обучения оказалось отнюдь не маленьким (было потрачено
приблизительно 36 часов машинного времени).
В другом эксперименте эта сеть обучалась на задаче ИСКЛЮЧАЮЩЕЕ
ИЛИ, которая была использована в качестве теста для сравнения с
другими алгоритмами. Для сходимости сети в среднем требовалось около
76 предъявлений обучающего множества. В качестве сравнения можно
указать, что при использовании обратного распространения в среднем
требовалось около 245 предъявлений для решения этой же задачи и 4986
итераций при использовании обратного распространения второго
порядка.
Ни одно из обучений не привело к локальному минимуму. Более того,
ни одно из 160 обучений не обнаружило неожиданных патологий, сеть
всегда правильно обучалась.
Эксперименты же с чистой машиной Коши потребовали значительно
большх времен обучения. Например, при  для
обучения сети в среднем требовалось около 2284 предъявлений
обучающего множества. для
обучения сети в среднем требовалось около 2284 предъявлений
обучающего множества.
Несмотря на такие обнадеживающие результаты, метод еще не
исследован до конца, особенно на больших задачах. Значительно
большая работа потребуется для определения его достоинств и
недостатков.
|




