|
Сети, рассмотренные на предыдущих лекциях, не имели обратных связей, т. е. связей, идущих от
выходов сетей к их входам. Отсутствие обратной
связи гарантирует безусловную устойчивость сетей. (Они не
могут войти в режим, когда выход беспрерывно блуждает от состояния к
состоянию и не пригоден для использования.) Но это весьма
желательное качество достигается не бесплатно: сети без обратных связей обладают более ограниченными
возможностями по сравнению с сетями с обратными
связями. Так как сети с обратными
связями имеют пути, передающие сигналы от выходов к входам,
то отклик таких сетей является динамическим, т. е. после приложения
нового входа вычисляется выход и, передаваясь по сети обратной связи, модифицирует вход. Затем выход
повторно вычисляется, и процесс повторяется снова и снова. Для
устойчивой сети последовательные итерации приводят к все меньшим
изменениям выхода, пока в конце концов выход не становится
постоянным. Для многих сетей процесс никогда не заканчивается, такие
сети называют неустойчивыми. Неустойчивые сети обладают интересными
свойствами и изучались в качестве примера хаотических систем. Однако
такой большой предмет, как хаос, находится за пределами этого курса.
Вместо этого мы сконцентрируем свое внимание на устойчивых сетях, т.
е. на тех, которые в завершении процесса дают постоянный выход.
Проблема устойчивости ставила в тупик первых исследователей. Никто
не мог предсказать, какие из сетей будут устойчивыми, а какие будут
находиться в постоянном изменении. Более того, проблема
представлялась столь трудной, что многие исследователи были
настроены пессимистически относительно возможности ее решения. К
счастью, была получена теорема, описавшая подмножество сетей с обратными связями, выходы которых в конце
концов достигают устойчивого состояния. Это замечательное достижение
открыло дорогу дальнейшим исследованиям, и сегодня многие ученые
занимаются исследованием сложного поведения и возможностей этих
систем. Дж. Хопфилд сделал важный вклад как в теорию, так и в
применение систем с обратными связями.
Поэтому некоторые из конфигураций известны как сети Хопфилда.
Конфигурации сетей с обратными связями
Рассмотренный нами ранее персептрон относится к классу сетей с
направленным потоком распространения информации и не содержит обратных связей. На этапе функционирования
каждый нейрон выполняет свою функцию — передачу возбуждения другим
нейронам — ровно один раз. Динамика состояний нейронов является
неитерационной.
Несколько более сложной является динамика в сети Кохонена.
Конкурентное соревнование нейронов достигается путем итераций, в
процессе которых информация многократно передается между
нейронами.
В общем случае может быть рассмотрена нейронная сеть, содержащая
произвольные обратные связи, по которым
переданное возбуждение возвращается к данному нейрону, и он повторно
выполняет свою функцию. Наблюдения за биологическими локальными
нейросетями указывают на наличие множественных обратных связей. Нейродинамика в таких системах
становится итерационной. Это свойство существенно расширяет
множество типов нейросетевых архитектур, но одновременно приводит к
появлению новых проблем.
Неитерационная динамика состояний нейронов является, очевидно,
всегда устойчивой. Обратные связи могут
приводить к возникновению неустойчивостей, подобных тем,
которые возникают в усилительных радиотехнических системах при
положительной обратной связи. В нейронных
сетях неустойчивость проявляется в блуждающей смене состояний
нейронов, не приводящей к возникновению стационарных состояний. В
общем случае, ответ на вопрос об устойчивости динамики произвольной
системы с обратными связями крайне сложен
и до настоящего времени является открытым.
Остановимся на важном частном случае нейросетевой архитектуры,
для которой свойства устойчивости подробно исследованы. На рис.
8.1 показана сеть с обратными
связями, состоящая из двух слоев. Способ представления
несколько отличается от использованного в работе Хопфилда и других
сходных, но эквивалентен им с функциональной точки зрения, а также
хорошо связан с сетями, рассмотренными на предыдущих лекциях.
Нулевой слой, как и на предыдущих рисунках, не выполняет
вычислительной функции, а лишь распределяет выходы сети обратно на
входы. Каждый нейрон первого слоя вычисляет взвешенную сумму своих
входов, давая сигнал NET, который затем с помощью нелинейной функции
F преобразуется в сигнал OUT. Эти операции сходны с нейронами других
сетей.
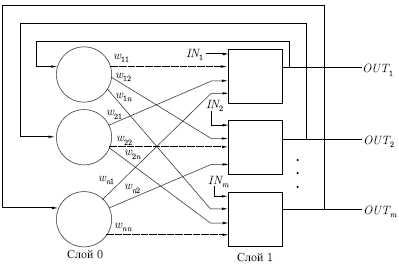
Рис. 8.1.
Бинарные системы
В первой работе Д.Хопфилда функция  была просто пороговой функцией. Выход такого нейрона равен единице,
если взвешенная сумма выходов с других нейронов больше порога
была просто пороговой функцией. Выход такого нейрона равен единице,
если взвешенная сумма выходов с других нейронов больше порога 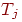 , в противном случае она равна нулю. Порог вычисляется
следующим образом: , в противном случае она равна нулю. Порог вычисляется
следующим образом:
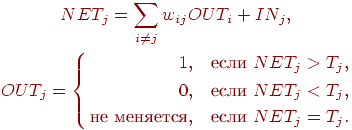
Состояние сети — это просто множество текущих значений
сигналов OUT от всех нейронов. В первоначальной сети Хопфилда состояние каждого нейрона
менялось в дискретные случайные моменты времени, в последующей
состояния нейронов могли меняться одновременно. Так как выходом
бинарного нейрона может быть только ноль или единица (промежуточных
уровней нет), то текущее состояние сети является двоичным числом,
каждый бит которого является сигналом OUT некоторого нейрона.
Задачи, решаемые данной сетью, как правило, формулируются
следующим образом. Известен некоторый набор двоичных сигналов
(изображений, оцифровок звука, прочих данных, описывающих некие
объекты или характеристики процессов), которые считаются
образцовыми. Сеть должна уметь из произвольного неидеального
сигнала, поданного на ее вход, выделить ("вспомнить" по частичной
информации) соответствующий образец (если такой есть) или "дать
заключение" о том, что входные данные не соответствуют ни одному из
образцов. В общем случае, любой сигнал может быть описан вектором
 , ,  —
число нейронов в сети и размерность входных и выходных векторов.
Каждый элемент —
число нейронов в сети и размерность входных и выходных векторов.
Каждый элемент 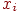 равен либо 1, либо 0. Обозначим вектор, описывающий k-й образец,
через
равен либо 1, либо 0. Обозначим вектор, описывающий k-й образец,
через  , а его компоненты, соответственно, — , а его компоненты, соответственно, — 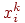 , ,  , ,  —
число образцов. Когда сеть распознaет (или "вспомнит") какой-либо
образец на основе предъявленных ей данных, ее выходы будут содержать
именно его, то есть —
число образцов. Когда сеть распознaет (или "вспомнит") какой-либо
образец на основе предъявленных ей данных, ее выходы будут содержать
именно его, то есть 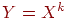 , где , где  --вектор выходных значений сети:
--вектор выходных значений сети:  . В
противном случае, выходной вектор не совпадет ни с одним
образцовым. . В
противном случае, выходной вектор не совпадет ни с одним
образцовым.
Если, например, сигналы представляют собой некие изображения, то,
отобразив в графическом виде данные с выхода сети, можно будет
увидеть картинку, полностью совпадающую с одной из образцовых (в
случае успеха) или же "вольную импровизацию" сети (в случае
неудачи).
На стадии инициализации сети весовые коэффициенты синапсов
устанавливаются следующим образом:
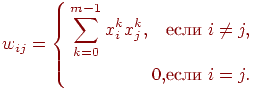
Здесь  и и 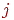 —
индексы, соответственно, предсинаптического и постсинаптического
нейронов; —
индексы, соответственно, предсинаптического и постсинаптического
нейронов; 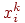 , , 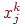 — —  -й
и -й
и 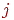 -й элементы вектора -й элементы вектора  -го образца. -го образца.
Алгоритм функционирования сети следующий (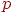 —
номер итерации): —
номер итерации):
-
На входы сети подается неизвестный сигнал. Фактически его ввод
осуществляется непосредственной установкой значений
аксонов: 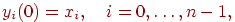
поэтому обозначение на схеме сети входных синапсов в явном виде
носит чисто условный характер. Ноль в скобке справа от 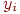 означает нулевую итерацию в цикле работы сети. означает нулевую итерацию в цикле работы сети.
-
Рассчитывается новое состояние нейронов:
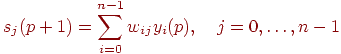
и новые значения аксонов 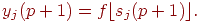
где  — активационная функция в виде скачка. — активационная функция в виде скачка.
- Проверка, изменились ли выходные значения аксонов за последнюю
итерацию. Если да — переход к пункту 2, иначе (если выходы
стабилизировались) — конец процедуры. При этом выходной вектор
представляет собой образец, наилучшим образом сочетающийся с
входными данными.
Как говорилось выше, иногда сеть не может провести распознавание
и выдает на выходе несуществующий образ. Это связано с проблемой
ограниченности возможностей сети. Для сети
Хопфилда число запоминаемых образов  не должно превышать величины, примерно равной
не должно превышать величины, примерно равной  . Кроме того, если два образа А и Б имеют
значительное сходство, они, возможно, будут вызывать у сети
перекрестные ассоциации, то есть предъявление на входы сети вектора
А приведет к появлению на ее выходах вектора Б и
наоборот. . Кроме того, если два образа А и Б имеют
значительное сходство, они, возможно, будут вызывать у сети
перекрестные ассоциации, то есть предъявление на входы сети вектора
А приведет к появлению на ее выходах вектора Б и
наоборот.
Когда нет необходимости, чтобы сеть выдавала образец в явном виде
и достаточно, скажем, получать номер образца, ассоциативную память
успешно реализует сеть Хэмминга. Данная
сеть характеризуется, по сравнению с сетью
Хопфилда, более экономным использованием памяти и меньшим
объемом вычислений, что становится очевидным из ее структуры (см. рис.
8.2).
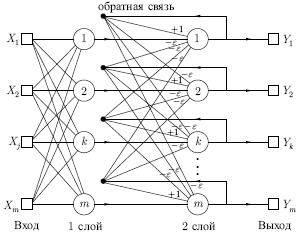
Рис. 8.2.
Сеть состоит из двух слоев. Первый и второй слои имеют по  нейронов, где
нейронов, где  —
число образцов. Нейроны первого слоя имеют по —
число образцов. Нейроны первого слоя имеют по  синапсов, соединенных с входами сети (которые образуют фиктивный
нулевой слой). Нейроны второго слоя связаны между собой
ингибиторными (отрицательными обратными)
синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с
его же аксоном.
синапсов, соединенных с входами сети (которые образуют фиктивный
нулевой слой). Нейроны второго слоя связаны между собой
ингибиторными (отрицательными обратными)
синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с
его же аксоном.
Идея работы сети состоит в нахождении расстояния Хэмминга от
тестируемого образа до всех образцов. Расстоянием Хэмминга
называется число отличающихся битов в двух бинарных векторах. Сеть
должна выбрать образец с минимальным расстоянием Хэмминга до
неизвестного входного сигнала, в результате чего будет активизирован
только один выход сети, соответствующий именно этому образцу.
На стадии инициализации весовым коэффициентам первого слоя и
порогу активационной функции присваиваются следующие
значения: 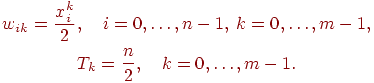
Здесь 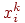 - -  -й
элемент -й
элемент  -го образца. -го образца.
Весовые коэффициенты тормозящих синапсов во втором слое берут
равными некоторой величине 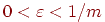 .
Синапс нейрона, связанный с его же аксоном, имеет вес +1. .
Синапс нейрона, связанный с его же аксоном, имеет вес +1.
Алгоритм функционирования сети
Хэмминга следующий:
-
На входы сети подается неизвестный вектор 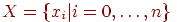 , ,
исходя из которого рассчитываются состояния нейронов первого
слоя (верхний индекс в скобках указывает номер слоя):
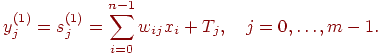
После этого полученными значениями инициализируются значения
аксонов второго слоя:
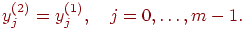
-
Вычисляются новые состояния нейронов второго слоя:
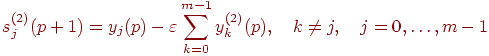
и значения их аксонов: 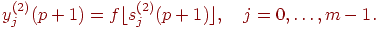
Активационная функция  имеет вид порога, причем величина
имеет вид порога, причем величина  должна быть достаточно большой, чтобы любые возможные значения
аргумента не приводили к насыщению.
должна быть достаточно большой, чтобы любые возможные значения
аргумента не приводили к насыщению.
- Проверить, изменились ли выходы нейронов второго слоя за
последнюю итерацию. Если да — перейти к шагу 2. Иначе — конец
процедуры.
Из оценки алгоритма видно, что роль первого слоя весьма условна:
воспользовавшись один раз на шаге 1 значениями его весовых
коэффициентов, сеть больше не обращается к нему, поэтому первый слой
может быть вообще исключен из сети.
Устойчивость
Как и в других сетях, веса между слоями в этой сети могут
рассматриваться в виде матрицы 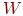 .
Сеть с обратными связями является
устойчивой, если ее матрица симметрична и имеет нули на главной
диагонали, т. е. если .
Сеть с обратными связями является
устойчивой, если ее матрица симметрична и имеет нули на главной
диагонали, т. е. если  и и 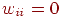 для всех для всех  . .
Устойчивость такой сети может быть доказана с помощью элегантного
математического метода. Допустим, что найдена функция, которая
всегда убывает при изменении состояния сети. В конце концов, эта
функция должна достичь минимума и прекратить изменение, гарантируя
тем самым устойчивость сети. Такая функция, называемая функцией
Ляпунова, для рассматриваемых сетей с обратными
связями может быть введена следующим образом:
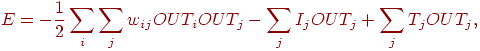
где  — искусственная энергия сети; — искусственная энергия сети;  — вес от выхода нейрона — вес от выхода нейрона  к
входу нейрона к
входу нейрона 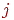 ; ;
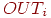 — выход нейрона — выход нейрона 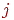 ; ;
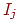 — внешний вход нейрона
— внешний вход нейрона 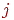 ; ;
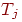 — порог нейрона
— порог нейрона 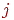 . .
Изменение энергии  ,
вызванное изменением состояния ,
вызванное изменением состояния 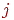 -нейрона, есть -нейрона, есть
![\delta E=\left[\sum_{i\ne j}(w_{ij}OUT_i)+I_j-T_j\right]\delta OUT_j=
-[NET_j-T_j]\delta OUT_j,](25455287ef36ac82fb47de2330a4f3d7.png)
где 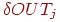 —
изменение выхода —
изменение выхода 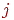 -го нейрона. -го нейрона.
Допустим, что величина NET нейрона 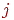 больше порога. Тогда выражение в скобках будет положительным, а из
данных уравнений следует, что выход нейрона
больше порога. Тогда выражение в скобках будет положительным, а из
данных уравнений следует, что выход нейрона 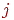 должен измениться в положительную сторону (или остаться без
изменения). Это значит, что
должен измениться в положительную сторону (или остаться без
изменения). Это значит, что 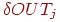 может
быть только положительным или нулем и может
быть только положительным или нулем и  должно быть отрицательным. Следовательно, энергия сети
должна либо уменьшиться, либо остаться без изменения. должно быть отрицательным. Следовательно, энергия сети
должна либо уменьшиться, либо остаться без изменения.
Далее, допустим, что величина  меньше порога. Тогда величина
меньше порога. Тогда величина  может
быть только отрицательной или нулем. Следовательно, опять энергия
должна уменьшиться или остаться без изменения. может
быть только отрицательной или нулем. Следовательно, опять энергия
должна уменьшиться или остаться без изменения.
И окончательно, если величина  равна порогу,
равна порогу, 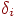 равна нулю и энергия остается без изменения. равна нулю и энергия остается без изменения.
Мы показали, что любое изменение состояния нейрона либо уменьшит
энергию, либо оставит ее без изменения. Благодаря такому
непрерывному стремлению к уменьшению энергия, в конце концов, должна
достигнуть минимума и прекратить изменение. По определению такая
сеть является устойчивой.
Симметрия сети является достаточным, но не необходимым условием
для устойчивости системы. Имеется много устойчивых систем (например,
все сети прямого действия), которые ему не удовлетворяют. Можно
продемонстрировать примеры, в которых незначительное отклонение от
симметрии будет приводить к непрерывным осцилляциям. Однако
приближенной симметрии обычно достаточно для устойчивости
систем.
Ассоциативность памяти и задача распознавания образов
Динамический процесс последовательной смены состояний нейронной
сети Хопфилда завершается в некотором
стационарном состоянии, являющимся локальным минимумом
энергетической функции 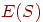 . Невозрастание энергии в процессе динамики приводит к
выбору такого локального минимума . Невозрастание энергии в процессе динамики приводит к
выбору такого локального минимума  ,
в бассейн притяжения которого попадает начальное состояние
(исходный, предъявляемый сети образ) ,
в бассейн притяжения которого попадает начальное состояние
(исходный, предъявляемый сети образ) 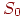 . В этом случае также говорят, что состояние . В этом случае также говорят, что состояние 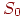 находится в чаше минимума
находится в чаше минимума  . .
При последовательной динамике в качестве стационарного состояния
будет выбран такой образ  ,
который потребует минимального числа изменений состояний отдельных
нейронов. Поскольку для двух двоичных векторов минимальное число
изменений компонент, переводящее один вектор в другой, является
расстоянием Хемминга ,
который потребует минимального числа изменений состояний отдельных
нейронов. Поскольку для двух двоичных векторов минимальное число
изменений компонент, переводящее один вектор в другой, является
расстоянием Хемминга 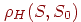 , то можно заключить, что динамика сети заканчивается в
ближайшем по Хеммингу локальном минимуме энергии. , то можно заключить, что динамика сети заканчивается в
ближайшем по Хеммингу локальном минимуме энергии.
Пусть состояние  соответствует некоторому идеальному образу памяти. Тогда эволюцию от
состояния
соответствует некоторому идеальному образу памяти. Тогда эволюцию от
состояния 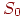 к состоянию к состоянию  можно сравнить с процедурой постепенного восстановления идеального
образа
можно сравнить с процедурой постепенного восстановления идеального
образа  по его искаженной (зашумленной или неполной) копии по его искаженной (зашумленной или неполной) копии 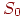 . Память с такими свойствами процесса считывания информации
является ассоциативной. При поиске искаженные части целого
восстанавливаются по имеющимся неискаженным частям на основе
ассоциативных связей между ними. . Память с такими свойствами процесса считывания информации
является ассоциативной. При поиске искаженные части целого
восстанавливаются по имеющимся неискаженным частям на основе
ассоциативных связей между ними.
Ассоциативный характер памяти сети
Хопфилда качественно отличает ее от обычной, адресной,
компьютерной памяти. В последней извлечение необходимой информации
происходит по адресу ее начальной точки (ячейки памяти).
Потеря адреса (или даже одного бита адреса) приводит к потере
доступа ко всему информационному фрагменту. При использовании же
ассоциативной памяти доступ к информации производится
непосредственно по ее содержанию, т.е. по частично известным
искаженным фрагментам. Потеря части информации или ее зашумление не
приводит к катастрофическому ограничению доступа, если оставшейся
информации достаточно для извлечения идеального образа.
Поиск идеального образа по имеющейся неполной или зашумленной его
версии называется задачей распознавания образов. В нашей
лекции особенности решения этой задачи нейронной сетью Хопфилда будут продемонстрированы на
примерах, которые получены с использованием модели сети на
персональной ЭВМ.
В рассматриваемой модели сеть содержала 100 нейронов,
упорядоченных в матрицу  . Сеть обучалась по правилу Хебба на трех идеальных образах
— шрифтовых начертаниях латинских букв M, A и G (см. рис.
8.3). После обучения нейросети в качестве начальных состояний
нейронов предъявлялись различные искаженные версии образов, которые
в дальнейшем эволюционировали с последовательной динамикой к
стационарным состояниям. . Сеть обучалась по правилу Хебба на трех идеальных образах
— шрифтовых начертаниях латинских букв M, A и G (см. рис.
8.3). После обучения нейросети в качестве начальных состояний
нейронов предъявлялись различные искаженные версии образов, которые
в дальнейшем эволюционировали с последовательной динамикой к
стационарным состояниям.

Рис. 8.3.
Для каждой пары изображений на рисунке
8.4, левый образ является начальным состоянием, а правый —
результатом работы сети, достигнутым стационарным состоянием.
Образ на рис.
8.4(А) был выбран для тестирования адекватности поведения на
идеальной задаче, когда предъявленное изображение точно
соответствует информации в памяти. В этом случае за один шаг было
достигнуто стационарное состояние. Образ на рис.
8.4(Б) характерен для задач распознавания текста независимо от
типа шрифта. Начальное и конечное изображения безусловно похожи, но
попробуйте это объяснить машине!
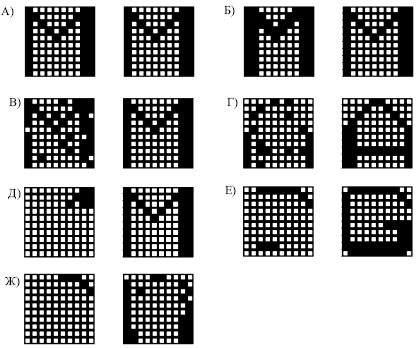
Рис. 8.4.
Задания на рис.
8.4(В, Г) характерны для практических приложений. Нейросетевая
система способна распознавать практически полностью зашумленные
образы. Задачи, соответствующие рисункам 8.4(Д,
Е), демонстрируют замечательное свойство сети Хопфилда: она способна ассоциативно
узнавать образ по его небольшому фрагменту. Важнейшей особенностью
работы сети является генерация ложных образов. Пример ассоциации к
ложному образу показан на рис.
8.4(Ж). Ложный образ является устойчивым локальным экстремумом
энергии, но не соответствует никакому идеальному образу. Он является
в некотором смысле собирательным образом, наследующим черты
идеальных собратьев. Ситуация с ложным образом эквивалентна нашему
"Где-то я уже это видел".
В данной простейшей задаче ложный образ является "неверным"
решением и поэтому вреден. Однако можно надеяться, что такая
склонность сети к обобщениям может быть как-то использована.
Характерно, что при увеличении объема полезной информации (сравните
рис.
8.4 (Е) и (Ж)) исходное состояние попадает в область притяжения
требуемого стационарного состояния, и образ распознается.
|




