Модификации правила Хэбба
Ограничения емкости синаптической памяти, а также проблема ложной
памяти классической нейронной сети в модели Хопфилда,
обученной по правилу Хебба, привели к появлению целого ряда
исследований, целью которых было снятие этих ограничений. При этом
главный упор делался на модификацию правил обучения.
Матрица Хебба с ортогонализацией образов
На предыдущей лекции было установлено, что ортогональность
образов обучающей выборки является весьма благоприятным
обстоятельством, так как в этом случае можно показать их устойчивое
сохранение в памяти. При точной ортогональности достигается
максимальная емкость памяти, равная 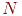 —
максимально возможному числу ортогональных образов из —
максимально возможному числу ортогональных образов из 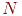 компонент.
компонент.
На этом свойстве ортогональных образов и основан один из наиболее
часто используемых способов улучшения правила Хебба: перед
запоминанием в нейронной сети исходные образы следует
ортогонализовать. Процедура ортогонализации приводит к новому виду
матрицы памяти:
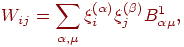
где  —
матрица, обратная к матрице —
матрица, обратная к матрице  : :
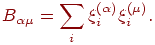
Такая форма матрицы памяти обеспечивает воспроизведение любого
набора из 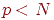 образов. Однако существенным недостатком этого метода является его
нелокальность: обучение связи между двумя нейронами требует
знания состояний всех других нейронов. Кроме того, прежде чем начать
обучение, необходимо заранее знать все обучающие образы.
Добавление нового образа требует полного переобучения сети. Поэтому
данный подход весьма далек от исходных биологических оснований сети Хопфилда—Хебба, хотя на практике приводит
к заметным улучшениям ее функционирования.
образов. Однако существенным недостатком этого метода является его
нелокальность: обучение связи между двумя нейронами требует
знания состояний всех других нейронов. Кроме того, прежде чем начать
обучение, необходимо заранее знать все обучающие образы.
Добавление нового образа требует полного переобучения сети. Поэтому
данный подход весьма далек от исходных биологических оснований сети Хопфилда—Хебба, хотя на практике приводит
к заметным улучшениям ее функционирования.
Отказ от симметрии синапсов
Другим подходом для улучшения правила Хебба является отказ от
симметрии синаптических соединений. Матрица памяти может выбираться
в следующей форме:
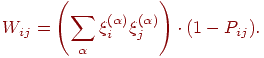
Элементы матрицы 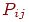 из множества из множества 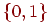 управляют наличием или отсутствием связи от нейрона управляют наличием или отсутствием связи от нейрона  к
нейрону к
нейрону 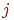 . .
Увеличение емкости памяти в этой модели в принципе может быть
достигнуто за счет появления новых степеней свободы, связанных с
матрицей  . В общем случае, однако, трудно предложить алгоритм выбора
этой матрицы. Следует также отметить, что динамическая система с
несимметричной матрицей не обязана быть устойчивой. . В общем случае, однако, трудно предложить алгоритм выбора
этой матрицы. Следует также отметить, что динамическая система с
несимметричной матрицей не обязана быть устойчивой.
Алгоритмы разобучения (забывания)
Возможность забывания ненужной, лишней информации является одним
из замечательных свойств биологической памяти. Идея приложения этого
свойства к искусственной нейросети Хопфилда "удивительно"
проста: при запоминании образов обучающей выборки вместе с ними
запоминаются и ложные образы. Их-то и следует "забыть".
Соответствующие алгоритмы получили название алгоритмов
разобучения. Суть их сводится к следующему.
На первой фазе происходит обучение сети по стандартному правилу
Хебба. Память наполняется истинными образами и множеством ложной
информации. На следующей фазе (фазе разобучения) сети предъявляется
некоторый (случайный) образ 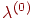 . Сеть эволюционирует от состояния . Сеть эволюционирует от состояния 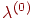 к некоторому состоянию к некоторому состоянию  , которое при большом объеме обучающей выборки чаще всего
оказывается ложным. Теперь матрица связей может быть поправлена, с
целью уменьшить глубину минимума энергии, отвечающего этому ложному
состоянию: , которое при большом объеме обучающей выборки чаще всего
оказывается ложным. Теперь матрица связей может быть поправлена, с
целью уменьшить глубину минимума энергии, отвечающего этому ложному
состоянию: 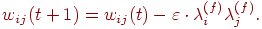
В качестве степени забывания 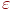 выбирается некоторое малое число, что гарантирует
незначительное ухудшение полезной памяти, если состояние выбирается некоторое малое число, что гарантирует
незначительное ухудшение полезной памяти, если состояние  не окажется ложным. После нескольких "сеансов забывания"
свойства сети улучшаются. не окажется ложным. После нескольких "сеансов забывания"
свойства сети улучшаются.
Данная процедура пока не имеет формального теоретического
обоснования, однако на практике приводит к более регулярной
энергетической поверхности нейронной сети и к увеличению объема
бассейнов притяжения полезных образов.
Непрерывные системы
На предыдущей лекции была рассмотрена классическая модель
Хопфилда с двоичными нейронами. Изменение состояний нейронов во
времени описывалось детерминированными правилами, которые в заданный
момент времени однозначно определяли степень возбуждения всех
нейронов сети.
Хопфилд рассматривал модели с непрерывной активационной функцией
 ,
точнее моделирующей биологический нейрон. В общем случае это ,
точнее моделирующей биологический нейрон. В общем случае это  -образная или логистическая функция -образная или логистическая функция

где 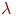 —
коэффициент, определяющий крутизну сигмоидальной функции. Если —
коэффициент, определяющий крутизну сигмоидальной функции. Если 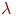 велико, велико,  приближается к описанной ранее пороговой функции. Небольшие значения
приближается к описанной ранее пороговой функции. Небольшие значения
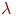 дают более пологий наклон. дают более пологий наклон.
Как и для бинарных систем, устойчивость гарантируется, если веса
симметричны, т.е.  и и 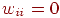 при всех при всех  .
Функция энергии, доказывающая устойчивость подобных систем,
сконструирована, но она не рассматривается здесь из-за своего
концептуального сходства с дискретным случаем. .
Функция энергии, доказывающая устойчивость подобных систем,
сконструирована, но она не рассматривается здесь из-за своего
концептуального сходства с дискретным случаем.
Если 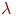 велико,
непрерывные системы функционируют подобно дискретным бинарным
системам, окончательно стабилизируясь со всеми выходами, близкими
нулю или единице, т. е. в вершине единичного гиперкуба. С
уменьшением велико,
непрерывные системы функционируют подобно дискретным бинарным
системам, окончательно стабилизируясь со всеми выходами, близкими
нулю или единице, т. е. в вершине единичного гиперкуба. С
уменьшением 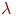 устойчивые точки удаляются от вершин, последовательно
исчезая по мере приближения устойчивые точки удаляются от вершин, последовательно
исчезая по мере приближения 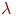 к нулю. На рис.
9.1 показаны линии энергетических уровней непрерывной системы с
двумя нейронами. к нулю. На рис.
9.1 показаны линии энергетических уровней непрерывной системы с
двумя нейронами.
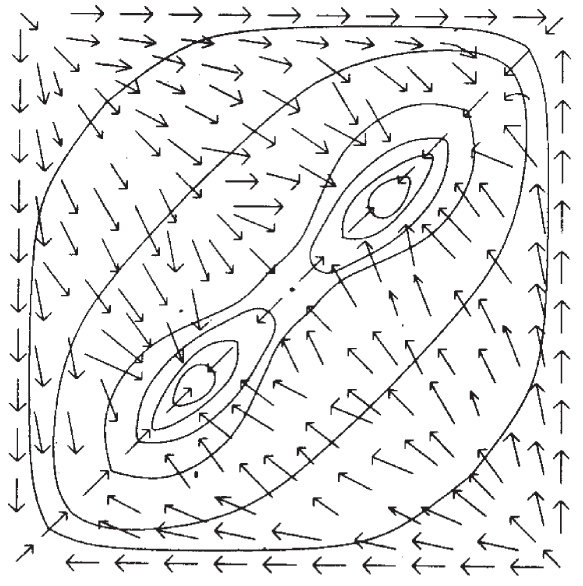
Рис. 9.1.
Сети Хопфилда и машина Больцмана
Недостатком сетей Хопфилда является их
тенденция стабилизироваться в локальном, а не в глобальном минимуме
функции энергии. Эта трудность преодолевается в основном с помощью
класса сетей, известных под названием машин
Больцмана, в которых изменения состояний нейронов обусловлены
статистическими, а не детерминированными закономерностями.
Существует тесная аналогия между этими методами и отжигом металла,
поэтому и сами методы часто называют имитацией отжига.
Термодинамические системы
Металл отжигают, нагревая его до температуры, превышающей точку
его плавления, а затем давая ему медленно остыть. При высоких
температурах атомы, обладая высокими энергиями и свободой
перемещения, случайным образом принимают все возможные конфигурации.
При постепенном снижении температуры энергии атомов уменьшаются, и
система в целом стремится принять конфигурацию с минимальной
энергией. Когда охлаждение завершено, достигается состояние
глобального минимума энергии.
При фиксированной температуре распределение энергий системы
определяется вероятностным фактором Больцмана 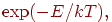
где  — энергия системы; — энергия системы;  —
постоянная Больцмана; —
постоянная Больцмана;  —
температура. —
температура.
Отсюда очевидно: имеется конечная вероятность того, что система
обладает высокой энергией даже при низких температурах. Сходным
образом имеется небольшая, но вычисляемая вероятность, что чайник с
водой на огне замерзнет, прежде чем закипеть.
Статистическое распределение энергий позволяет системе выходить
из локальных минимумов энергии. В то же время, вероятность
высокоэнергетических состояний быстро уменьшается со снижением
температуры. Следовательно, при низких температурах имеется сильная
тенденция занять низкоэнергетическое состояние.
Статистические сети Хопфилда
Если правила изменения состояний для бинарной сети Хопфилда заданы статистически, а не
детерминированно, то возникает система, имитирующая отжиг. Для ее
реализации вводится вероятность изменения веса как функция от
величины, на которую выход нейрона OUT превышает его порог.
Пусть 
где  — выход
NET нейрона — выход
NET нейрона  ; ;
 — порог нейрона — порог нейрона  ,
и ,
и
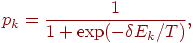
(отметим вероятностную функцию Больцмана в знаменателе), где  —
искусственная температура. —
искусственная температура.
В стадии функционирования искусственной температуре  приписывается большое значение, нейроны устанавливаются в начальном
состоянии, определяемом входным вектором, и сеть имеет возможность
искать минимум энергии в соответствии с нижеследующей
процедурой:
приписывается большое значение, нейроны устанавливаются в начальном
состоянии, определяемом входным вектором, и сеть имеет возможность
искать минимум энергии в соответствии с нижеследующей
процедурой:
- Приписать состоянию каждого нейрона с вероятностью
 значение единица, а с вероятностью значение единица, а с вероятностью  — нуль. — нуль.
- Постепенно уменьшать искусственную температуру и повторять шаг
1, пока не будет достигнуто равновесие.
Обобщенные сети
Принцип машины Больцмана может быть
перенесен на сети практически любой конфигурации, но без
гарантированной устойчивости. Достаточно выбрать одно множество
нейронов в качестве входов и другое множество в качестве выходов,
затем придать входному множеству значения входного вектора и
предоставить сети возможность релаксировать в соответствии с
описанными выше правилами 1 и 2.
Процедура обучения для такой сети состоит из следующих шагов:
-
Вычислить закрепленные вероятности:
а) придать входным и выходным нейронам значения обучающего
вектора;
б) предоставить сети возможность искать равновесие;
в) записать выходные значения для всех нейронов;
г) повторить шаги от а до в для всех обучающих векторов;
д) вычислить вероятность 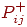 , т. е. по всему множеству обучающих векторов вычислить
вероятность того, что значения обоих нейронов равны единице. , т. е. по всему множеству обучающих векторов вычислить
вероятность того, что значения обоих нейронов равны единице.
-
Вычислить незакрепленные вероятности:
а) предоставить сети возможность "свободного движения" без
закрепления входов или выходов, начав со случайного состояния;
б) повторить шаг 2а много раз, регистрируя значения всех
нейронов;
в) вычислить вероятность 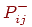 , т. е. вероятность того, что значения обоих нейронов
равны единице. , т. е. вероятность того, что значения обоих нейронов
равны единице.
-
Скорректировать веса сети следующим образом: 
где 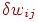 —
изменение веса —
изменение веса  , , 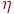 — коэффициент скорости обучения. — коэффициент скорости обучения.
Приложения
Аналого-цифровой преобразователь
Рассмотрим электрическую схему, которая основана на сети с
обратной связью и реализует четырехбитовый аналого-цифровой
преобразователь. На рис.
9.2 показана блок-схема этого устройства с усилителями,
выполняющими роль искусственных нейронов. Сопротивления, выполняющие
роль весов, соединяют выход каждого нейрона с входами всех
остальных. Чтобы удовлетворить условию устойчивости, выход нейрона
не соединялся сопротивлением с его собственным входом, а веса
брались симметричными, т. е. сопротивление от выхода нейрона  к
входу нейрона к
входу нейрона 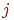 имело ту же величину, что и сопротивление от выхода нейрона
имело ту же величину, что и сопротивление от выхода нейрона 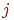 к
входу нейрона к
входу нейрона  . .
Заметим, что усилители имеют прямой и инвертированный выходы. Это
позволяет с помощью обычных положительных сопротивлений
реализовывать и те случаи, когда веса должны быть отрицательными. На
рис.
9.2 показаны все возможные сопротивления, при этом никогда не
возникает необходимости присоединять как прямой, так и
инвертированный выходы нейрона к входу другого нейрона.
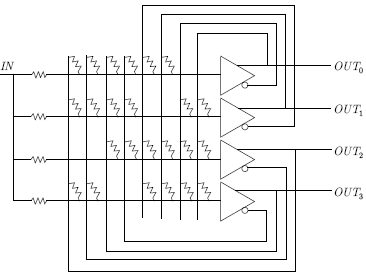
Рис. 9.2.
В реальной системе каждый усилитель обладает конечным входным
сопротивлением и входной емкостью, что должно учитываться при
расчете динамических характеристик. Для устойчивости сети не
требуется равенства этих параметров для всех усилителей и их
симметричности. Так как эти параметры влияют лишь на затраченное для
получения решения время, а не на само решение, для упрощения анализа
они исключены.
Предполагается, что используется пороговая функция (предел
сигмоидальной функции при 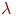 , стремящемся к бесконечности). Далее, все выходы
изменяются в начале дискретных интервалов времени, называемых
эпохами. В начале каждой эпохи исследуется сумма входов каждого
нейрона. Если она больше порога, выход принимает единичное значение,
если меньше — нулевое. На протяжении эпохи выходы нейронов не
изменяются. , стремящемся к бесконечности). Далее, все выходы
изменяются в начале дискретных интервалов времени, называемых
эпохами. В начале каждой эпохи исследуется сумма входов каждого
нейрона. Если она больше порога, выход принимает единичное значение,
если меньше — нулевое. На протяжении эпохи выходы нейронов не
изменяются.
Целью является такой выбор сопротивлений (весов), чтобы
непрерывно растущее напряжение  ,
приложенное к одновходовому терминалу, порождало множество из
четырех выходов, представляющих двоичную запись числа, величина
которого приближенно равна входному напряжению (см. рис.
9.3). Определим сначала функцию энергии следующим образом: ,
приложенное к одновходовому терминалу, порождало множество из
четырех выходов, представляющих двоичную запись числа, величина
которого приближенно равна входному напряжению (см. рис.
9.3). Определим сначала функцию энергии следующим образом:
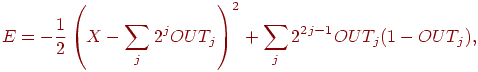
где  — входное напряжение. — входное напряжение.
Когда  минимизировано, то получаются нужные выходы. Первое
выражение в скобках минимизируется, когда двоичное число,
образованное выходами, наиболее близко (в среднеквадратичном смысле)
к аналоговой величине входа минимизировано, то получаются нужные выходы. Первое
выражение в скобках минимизируется, когда двоичное число,
образованное выходами, наиболее близко (в среднеквадратичном смысле)
к аналоговой величине входа  .
Второе выражение в скобках обращается в нуль, когда все выходы равны
1 или 0, тем самым накладывая ограничение, что выходы принимают
только двоичные значения. .
Второе выражение в скобках обращается в нуль, когда все выходы равны
1 или 0, тем самым накладывая ограничение, что выходы принимают
только двоичные значения.
Если данное уравнение перегруппировать, то получим следующее
выражение для весов: 
где  —
проводимость (величина, обратная сопротивлению) от выхода нейрона —
проводимость (величина, обратная сопротивлению) от выхода нейрона
 к
входу нейрона к
входу нейрона 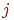 (равная также проводимости от выхода нейрона
(равная также проводимости от выхода нейрона 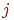 к
входу нейрона к
входу нейрона  ); );
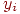 — проводимость от входа
— проводимость от входа  к
входу нейрона к
входу нейрона  .
Чтобы получить схему с приемлемыми значениями сопротивлений и
потребляемой мощности, все веса должны быть промасштабированы. .
Чтобы получить схему с приемлемыми значениями сопротивлений и
потребляемой мощности, все веса должны быть промасштабированы.
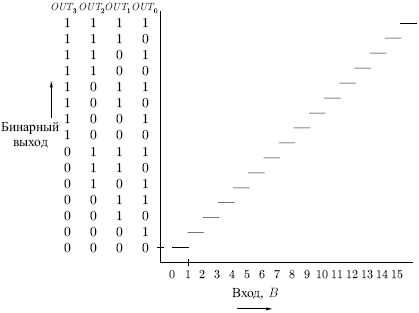
Рис. 9.3.
Идеальная выходная характеристика, изображенная на рис.
9.3, будет реализована лишь в том случае, если входы
устанавливаются в нуль перед выполнением преобразования. Если этого
не делать, сеть может попасть в локальный минимум энергии и дать
неверный выход.
Задача коммивояжера
Задача коммивояжера является оптимизационной задачей, часто
возникающей на практике. Она может быть сформулирована следующим
образом: для некоторой группы городов с заданными расстояниями между
ними требуется найти кратчайший маршрут с посещением каждого города
один раз и с возвращением в исходную точку. Было доказано, что эта
задача принадлежит большому множеству задач, называемых "NP-полными"
(недетерминистски полиномиальными). Для NP-полных задач не известно
лучшего метода решения, чем полный перебор всех возможных вариантов,
и, по мнению большинства математиков, маловероятно, чтобы лучший
метод был когда-либо найден. Так как такой полный поиск практически
неосуществим для большого числа городов, то эвристические методы
используются для нахождения приемлемых, хотя и неоптимальных
решений.
Существует решение этой задачи, основанное на сетях с обратными
связями. Допустим, что города, которые необходимо посетить, помечены
буквами 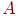 , ,  , ,
 и и
 ,
а расстояния между парами городов есть ,
а расстояния между парами городов есть  , ,  и т.д. и т.д.
Решением является упорядоченное множество из  городов. Задача состоит в отображении его в вычислительную сеть с
использованием нейронов в режиме с большой крутизной характеристики
(
городов. Задача состоит в отображении его в вычислительную сеть с
использованием нейронов в режиме с большой крутизной характеристики
(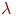 приближается к бесконечности). Каждый город представлен строкой из
приближается к бесконечности). Каждый город представлен строкой из
 нейронов. Выход одного и только одного нейрона из них равен единице
(все остальные равны нулю). Этот равный единице выход нейрона
показывает порядковый номер, в котором данный город посещается при
обходе. В табл. 23.1 приведен случай, когда город
нейронов. Выход одного и только одного нейрона из них равен единице
(все остальные равны нулю). Этот равный единице выход нейрона
показывает порядковый номер, в котором данный город посещается при
обходе. В табл. 23.1 приведен случай, когда город  посещается первым, город
посещается первым, город 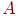 —
вторым, город —
вторым, город  —
третьим и город —
третьим и город  —
четвертым. Для такого представления требуется —
четвертым. Для такого представления требуется  нейронов — число, которое быстро растет с увеличением числа городов.
Длина полученного маршрута была бы равна
нейронов — число, которое быстро растет с увеличением числа городов.
Длина полученного маршрута была бы равна  . Так
как каждый город посещается только один раз, и в каждый момент
посещается лишь один город, то в каждой строке и в каждом столбце
имеется по одной единице. Для задачи с . Так
как каждый город посещается только один раз, и в каждый момент
посещается лишь один город, то в каждой строке и в каждом столбце
имеется по одной единице. Для задачи с  городами всего имеется
городами всего имеется 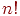 различных маршрутов обхода. Если
различных маршрутов обхода. Если  , то имеется , то имеется 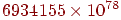 возможных маршрутов. Если принять во внимание, что в нашей галактике
(Млечном Пути) имеется лишь
возможных маршрутов. Если принять во внимание, что в нашей галактике
(Млечном Пути) имеется лишь 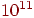 звезд, то станет ясным, что полный перебор всех возможных
маршрутов для 1000 городов даже на самом быстром в мире компьютере
займет время, сравнимое с геологической эпохой. звезд, то станет ясным, что полный перебор всех возможных
маршрутов для 1000 городов даже на самом быстром в мире компьютере
займет время, сравнимое с геологической эпохой.
| город |
Порядок
следования |
| 1 |
2 |
3 |
4 |
| A |
0 |
1 |
0 |
0 |
| B |
0 |
0 |
0 |
1 |
| C |
1 |
0 |
0 |
0 |
| D |
0 |
0 |
1 |
0 |
Продемонстрируем теперь, как сконструировать сеть для решения
этой NP-полной проблемы. Каждый нейрон снабжен двумя индексами,
которые соответствуют городу и порядковому номеру его посещения в
маршруте. Например, 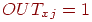 показывает, что город
показывает, что город  был
был 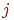 -м по порядку городом маршрута. -м по порядку городом маршрута.
Функция энергии должна удовлетворять двум требованиям: во-первых,
должна быть малой только для тех решений, которые имеют по одной
единице в каждой строке и в каждом столбце; во-вторых, должна
оказывать предпочтение решениям с короткой длиной маршрута.
Первое требование удовлетворяется введением следующей, состоящей
из трех сумм, функции энергии:
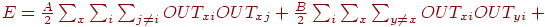
![+
\frac{C}{2}\left[\left(\sum_x\sum_iOUT_{xi}\right)-n\right]^2,](b2ffaa63e24e9bc8916077d0ac52949e.png)
где 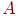 , ,  и и
 —
некоторые константы. Этим достигается выполнение следующих
условий: —
некоторые константы. Этим достигается выполнение следующих
условий:
- Первая тройная сумма равна нулю в том и только в том случае,
если каждая строка (город) содержит не более одной единицы.
- Вторая тройная сумма равна нулю в том и только в том случае,
если каждый столбец (порядковый номер посещения) содержит не более
одной единицы.
-
Третья сумма равна нулю в том и только в том случае, если
матрица содержит ровно  единиц. Второе требование — предпочтение коротких маршрутов —
удовлетворяется с помощью добавления следующего члена к функции
энергии:
единиц. Второе требование — предпочтение коротких маршрутов —
удовлетворяется с помощью добавления следующего члена к функции
энергии:
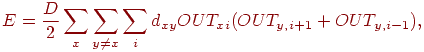
Заметим, что этот член представляет собой длину любого
допустимого маршрута. Для удобства индексы определяются по модулю
 ,
т. е. ,
т. е. 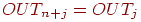 , a , a
 —
некоторая константа. —
некоторая константа.
При достаточно больших значениях 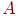 , ,
 и и
 низкоэнергетические состояния будут представлять допустимые
маршруты, а большие значения
низкоэнергетические состояния будут представлять допустимые
маршруты, а большие значения  гарантируют, что будет найден короткий маршрут.
гарантируют, что будет найден короткий маршрут.
Теперь зададим значения весов, т. е. установим соответствие между
членами в функции энергии и членами общей формы (см. уравнение
6.2).
Получаем
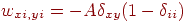 (не
допускает более одной единицы в строке) (не
допускает более одной единицы в строке)
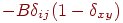 (не
допускает более одной единицы в столбце) (не
допускает более одной единицы в столбце)
 (глобальное ограничение) (глобальное ограничение)
 (член,
отвечающий за длину цикла), (член,
отвечающий за длину цикла),
где 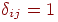 , если , если
 , в противном случае , в противном случае 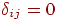 . Кроме
того, каждый нейрон имеет смещающий вес . Кроме
того, каждый нейрон имеет смещающий вес 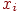 , соединенный с , соединенный с  и равный
и равный  . .
Был проведен эксперимент, в котором задача коммивояжера была
решена для 10 городов. В этом случае возбуждающая функция была
равна ![OUT=\frac12[1+\th(NET/U_0)].](bc860cbd5af7f340bbc80d8df776efcc.png)
Как показали результаты, 16 из 20 прогонов сошлись к допустимому
маршруту и около 50\% решений оказались кратчайшими маршрутами, что
было установлено с помощью полного перебора. Наш результат станет
более впечатляющим, если осознать, что имеется 181440 допустимых
маршрутов.
Обсуждение
Локальные минимумы
Сеть, выполняющая аналого-цифровое преобразование, всегда находит
единственное оптимальное решение. Это обусловлено простой природой
поверхности энергии в такой задаче. В задаче коммивояжера
поверхность энергии сильно изрезана, изобилует склонами, долинами и
локальными минимумами и нет гарантии, что будет найдено глобальное
оптимальное решение и что полученное решение будет допустимым. При
этом возникают серьезные сомнения относительно надежности сети и
доверия к ее решениям. Эти недостатки сети смягчаются тем
обстоятельством, что нахождение глобальных минимумов для NP-полных
задач является очень трудной задачей, которая не может быть решена в
приемлемое время никаким иным методом. Другие методы значительно
более медленны и дают не лучшие результаты.
Скорость
Главное достоинство сети — ее способность быстро производить
вычисления. Причина этого — высокая степень распараллеливания
вычислительного процесса. Если сеть реализована на аналоговой
электронике, то решение редко занимает промежуток времени, больший
нескольких постоянных времени сети. Более того, время сходимости
слабо зависит от размерности задачи. Для сравнения: при
использовании обычных подходов время, необходимое для решения,
возрастает более чем экспоненциально.
Функция энергии
Определение функции энергии сети в зависимости от задачи не
является тривиальным. Существующие решения были получены с помощью
изобретательности, математического опыта и таланта, которые не
родятся в изобилии.
Емкость сети
Актуальным предметом изучения остается максимальное количество
запоминаемой информации, которое может храниться в сети Хопфилда. Так как сеть из  двоичных нейронов может иметь
двоичных нейронов может иметь  состояний, то исследователи были удивлены, обнаружив, что
максимальная емкость памяти оказалась значительно меньшей.
состояний, то исследователи были удивлены, обнаружив, что
максимальная емкость памяти оказалась значительно меньшей.
Если бы удалось закрепить в памяти большое количество
информационных единиц, то сеть не стабилизировалась бы на некоторых
из них. Более того, она могла бы помнить то, чему ее не учили, т. е.
могла стабилизироваться на решении, не являющемся требуемым
вектором. Эти свойства ставили в тупик первых исследователей,
которые не имели математических методов для предварительной оценки
емкости памяти сети.
Последние результаты пролили свет на эту проблему. Например,
предполагалось, что максимальное количество запоминаемой информации,
которое может храниться в сети из 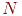 нейронов и безошибочно извлекаться, меньше чем
нейронов и безошибочно извлекаться, меньше чем 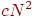 , где , где  —
положительная константа, большая единицы. Хотя этот предел и
достигается в некоторых случаях, в общем случае он оказался слишком
оптимистическим. Было экспериментально показано, что предельное
значение емкости обычно ближе к —
положительная константа, большая единицы. Хотя этот предел и
достигается в некоторых случаях, в общем случае он оказался слишком
оптимистическим. Было экспериментально показано, что предельное
значение емкости обычно ближе к 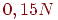 . Также, по новейшим данным, число таких состояний не может
превышать . Также, по новейшим данным, число таких состояний не может
превышать 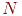 , что согласуется с наблюдениями над реальными системами и
является наилучшей на сегодняшний день оценкой. , что согласуется с наблюдениями над реальными системами и
является наилучшей на сегодняшний день оценкой.
|




