|
|
Разностные схемы Эйлера
В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения. Однако этот метод дает одновременно и способ нахождения искомой функции в табличной форме.
Пусть дано дифференциальное уравнение. Найти приближенное численное решение этого дифференциального уравнения, т.е. составить таблицу приближенных значений функции у=у(х) удовлетворяющей заданным начальным условиям.
|
x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
… |
xn |
|
y |
y0 |
y1 |
y2 |
y3 |
y4 |
y5 |
… |
yn |
Где, xi=x0+i×
h, 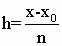 – шаг таблицы. – шаг таблицы.
Приближенно можно считать, что правая часть остается постоянной на каждом из отрезков между точками деления. Метод Эйлера состоит в непосредственной замене производной разностными отношениями по приближенной формуле:
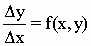
y-y0=f(x0,y0)×
(x-x0)
y=y0+f(x0,y0)×
(x-x0)
если x=x1, то
y1=y0+f(x0,y0)×
(x1-x0)
y1=y0+h×
f(x0,y0)
D
y0=h×
f(x0,y0)
если x=x2, то
y2=y1+f(x1,y1)×
(x2-x1)
y2=y1+h×
f(x1,y1)
D
y1=h×
f(x1,y1)
…
если x=xi+1, то
yi+1=yi+h×
f(xi,yi)
D
yi=h×
f(xi,yi)
Таким образом, получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом применении пары формул:
D
yk=h×
f(xk,yk)
yk+1=yk+D
yk
где k=0, 1, 2, … ,n
Геометрически эти формулы означают, что на отрезке [ xi, xi+1] интегральная кривая заменяется отрезком касательной к кривой (см. рис. 6.3, рис. 6.4).
|
|




