|
|
Численное интегрирование
Постановка задачи.
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида 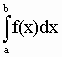 (1.1) (1.1)
где f(x) данная функция, непрерывная на отрезке [a; b]. Если функция f(x) задана формулой и мы умеем найти неопределенный интеграл F(x), то определенный интеграл вычисляется по формуле Ньютона-Лейбница:
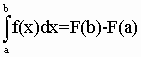 (1.2) (1.2)
Если же неопределенный интеграл данной функции мы найти не умеем, или по какой-либо причине не хотим воспользоваться формулой (1.2), или если функция f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла (1.1) существует много численных методов, из которых рассмотрим 6 основных:
метод правых, левых и средних прямоугольников, трапеций, Симпсона и Монте-Карло.
При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если f(x)³
0 на отрезке [a; b], то 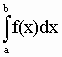 численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1). численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1).
Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.
|
|




