|
|
Метод трапеций
Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка 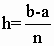 . Точки деления будут: x0=a; x1=a+h; x2=a+2×
h, ... , xn-1=a+(n-1)×
h; xn=b. Эти числа будем называть узлами. Вычислим значения функции f(x) в узлах, обозначим их y0, y1, y2, ... , yn. Cтало быть, y0=f(a), y1=f(x1), y2=f(x2), ... , yn=f(b). Числа y0, y1, y2, ... , yn являются ординатами точек графика функции, соответствующих абсциссам x0, x1, x2, ... , xn
Формула трапеций :
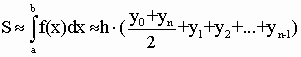
Формула означает, что площадь криволинейной трапеции заменяется площадью многоугольника, составленного из n трапеций (рис. 1); при этом кривая заменяется вписанной в нее ломаной.
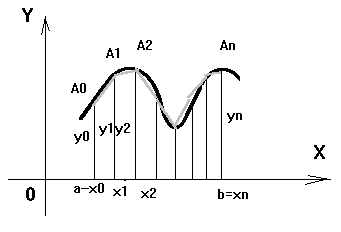
Рис. 1
|
|
