Постановка задачи интерполирования
Приближение функций
Для некоторой функции 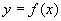 на отрезке
на отрезке 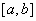 определена таблица ее значений в конечном числе точек этого отрезка
определена таблица ее значений в конечном числе точек этого отрезка 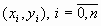 , где
, где 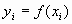 ,
, 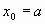 ,
, 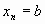 ,
, 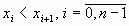 . Такой способ задания функций называется табличным. Например, таблицы Брадиса.
. Такой способ задания функций называется табличным. Например, таблицы Брадиса.
Интерполяция заключается в нахождении по таблице значений функции 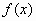 ее приближенного аналитического выражения
ее приближенного аналитического выражения 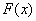 , приближающего функцию
, приближающего функцию 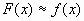 на отрезке
на отрезке 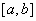 , причем
, причем 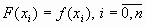 . Это позволяет получить приближенное значение функции
. Это позволяет получить приближенное значение функции 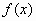 в любой точке отрезка
в любой точке отрезка 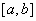 , а не только в точках таблицы.
, а не только в точках таблицы.
Приближение одной функции другой
Аналитическое выражение для функции 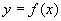 известно и является слишком сложным, а функция должна подвергаться различным математическим операциям. Если функция
известно и является слишком сложным, а функция должна подвергаться различным математическим операциям. Если функция 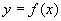 хорошо приближается многочленами, то также используется интерполяция.
хорошо приближается многочленами, то также используется интерполяция.
Планирование эксперимента
При минимальном количестве измерений определить наилучшее приближение функции 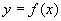 . Возможно, также получение значений функции
. Возможно, также получение значений функции 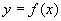 из экспериментальных данных, так что получение других промежуточных значений может оказаться затруднительным или невозможным, а аналитическое выражении функции
из экспериментальных данных, так что получение других промежуточных значений может оказаться затруднительным или невозможным, а аналитическое выражении функции 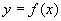 неизвестным.
неизвестным.
Если интерполяционная функция – многочлен, то задача интерполяции может быть сформулирована следующим образом. Для данных значений 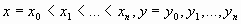 найти многочлен
найти многочлен 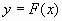 степени
степени 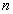 , удовлетворяющий условиям
, удовлетворяющий условиям
|
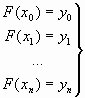 , ,
|
((1) |
где точки
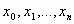 - узлы интерполяции, а многочлен
- узлы интерполяции, а многочлен 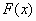 степени
степени 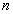 - интерполяционный многочлен.
- интерполяционный многочлен.
1. Непрерывная на отрезке функция может быть как угодно хорошо приближена на этом отрезке многочленом (которых существует бесконечно много).
2. Для заданных на плоскости
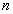 точек с различными абсциссами существует единственный полином степени не выше
точек с различными абсциссами существует единственный полином степени не выше 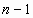 , который проходит через все эти точки.
, который проходит через все эти точки.
Гладкая функция порядка
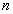 – функция, имеющая на множестве задания производные порядка
– функция, имеющая на множестве задания производные порядка 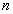 , причем
, причем 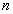 -ая производная непрерывна.
-ая производная непрерывна.
Гладкая линия
– линия, если функции ее параметрического задания непрерывно дифференцируемы на заданном промежутке и в любой его точке одновременно не обращаются в 0.
Кусочно-гладкая линия
– линия, которую можно разбить на конечное число гладких линий.
Геометрически задача отыскания функции
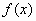 по заданным ее частным значениям означает построение кривой, проходящей через точки плоскости с координатами
по заданным ее частным значениям означает построение кривой, проходящей через точки плоскости с координатами 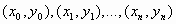 . Через заданные точки можно провести бесчисленное множество различных кривых, поэтому вводятся дополнительные ограничения, чтобы задача приобрела более определенный характер.
. Через заданные точки можно провести бесчисленное множество различных кривых, поэтому вводятся дополнительные ограничения, чтобы задача приобрела более определенный характер.




