|
|
Интерполяция многочленом Лагранжа
Из постановки задачи интерполяции следует, что многочлен 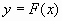 степени степени 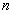 можно записать в виде можно записать в виде 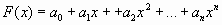 . Для каждого узла интерполяции записывается такой многочлен и получается система линейных уравнений . Для каждого узла интерполяции записывается такой многочлен и получается система линейных уравнений
Вместо решения СЛУ (1) непосредственно (определитель матрицы коэффициентов (2) – определитель Вандермонда), строится многочлен 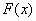 , удовлетворяющий всем поставленным условиям. , удовлетворяющий всем поставленным условиям.
Выражение многочлена, принимающего в точке 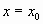 значение значение 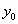 , а в других точках обращающегося в ноль, будет следующее , а в других точках обращающегося в ноль, будет следующее
|
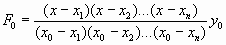
|
(3) |
Аналогично, для точки 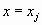 , , 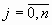
|
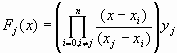 , , 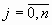
|
(4) |
Искомый многочлен Лагранжа определяется формулой
|
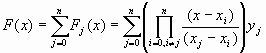
|
(5) |
Многочлен (5) удовлетворяет всем поставленным условиям.
Достоинства метода:
- график интерполяционного многочлена Лагранжа проходит через каждую точку;
- простота описания;
- однозначное определение;
- построенная функция имеет непрерывные производные любого порядка.
Простота описания и однозначность задания набором своих коэффициентов являются несомненными достоинствами данного интерполяционного многочлена. Наряду с достоинствами, данный многочлен обладает недостатками. Например, степень многочлена зависит от количества узлов интерполяции – на единицу меньше, что может привести к значительным отклонениям. Также, существенным недостатком является то, что изменение одной точки требует полного перерасчета и к значительным изменениям вида многочлена.
|
|




