|
|
Рекуррентные соотношения
Последовательность чисел или функций, в которой каждый следующий член выражается через предыдущий, называется рекуррентной, а формулы, устанавливающие эту связь, - рекуррентными соотношениями. Рекуррентные соотношения удобно использовать при составлении алгоритмов вычисления величин, при этом нет необходимости хранить все промежуточные значения. В выражении следующего значения некоторой величины через ее предыдущие значения и состоит суть метода рекуррентных соотношений.
Если последовательность чисел или функций конечна, то для нахождения значений функций (например, суммы, произведения или n-ого члена ) используется арифметический цикл, т.е. цикл, в котором заранее известно число повторений. Трудность при решении таких задач представляет нахождение самой рекуррентной формулы. Я предлагаю ученикам общий подход к получению рекуррентной формулы, опираясь на метод математической индукции.
Вывод рекуррентной формулы
При решении задач на вычисление сумм (произведений) членов конечных или бесконечных последовательностей, вычисления пределов последовательностей наибольшую трудность представляет получение рекуррентной формулы. Далеко не во всех задачах закономерность, связывающая предыдущий и последующий члены последовательности, очевидна, как, например, в последовательности
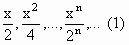
Любой член последовательности можно выразить как предыдущий умноженный на 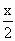 , т. е. аn+1=аn , т. е. аn+1=аn 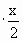 . .
А вот в последовательности

выражение, связывающее следующий член с предыдущим, уже не так очевидно. В таком случае я показываю общую схему получения рекуррентной формулы.
Запишем формулу для любого члена последовательности (2)
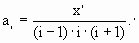
Тогда n-ый член последовательности принимает вид:
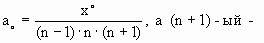 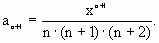  
. Разделим ( n+1)-ый член на n-ый.
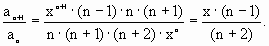
В результате получим знаменатель последовательности, т.е. тот множитель, который связывает следующий член последовательности с предыдущим.
Следовательно, рекуррентная формула имеет вид 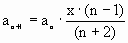
Правильность полученной формулы доказывается индукцией.
Проверим, действительно ли по этой формуле получаем члены последовательности, идущие подряд.
При n=1 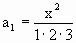
При n=2 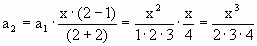
При n=3 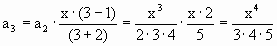 и т.д. и т.д.
Полученная формула действительно формирует члены последовательности.
В качестве примера решим задачу.
|
|




