|
|
Метод Рунге-Кутта второго порядка (Метод Эйлера-Коши)
Рассмотрим метод Рунге-Кутта второго порядка. В этом методе величины y i+1 вычисляются по следующим формулам:
yi+1 = yi + D
yi
D
yi=D
yi1+D
yi2
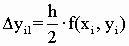 , ,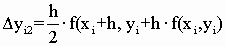
См. рис. 1
Тогда 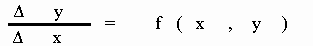 . .
Обозначим 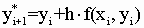 , тогда , тогда 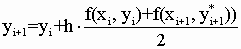
Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке ( xi, yi) и во вспомогательной точке 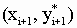 , а в качестве окончательного берем среднее из этих направлений. , а в качестве окончательного берем среднее из этих направлений.
Метод Рунге-Кутта четвертого порядка
В вычислительной практике наиболее часто используется метод Рунге-Кутта четвертого порядка.
В этом методе величины y i+1 вычисляются по следующим формулам:
yi+1 = yi + D
yi
D
yi=h×
(k1 + 2k2 + 2k3 + k4)/6, i = 0, 1, ...
k1 = f(xi, yi),
k2 = f(xi+h/2, yi+h×
k1/2),
k3 = f(xi+h/2, yi+h×
k2/2),
k4 = f(xi+h, yi+h×
k3).

|
|




