|
|
Интерполяционные кубические сплайны
Интерполяционный кубический сплайн – функция 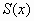 , обладающая следующими свойствами: , обладающая следующими свойствами:
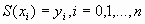 ;
на каждом отрезке ;
на каждом отрезке 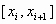 , , 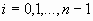 , функция , функция 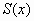 имеет вид имеет вид
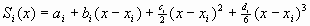 , , 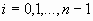 ; ;
на всем отрезке задания 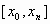 функция функция 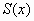 имеет непрерывную вторую производную.
имеет непрерывную вторую производную.
Так как сплайн 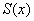 на каждом из отрезков на каждом из отрезков 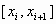 определяется четырьмя коэффициентами, то для его полного построения на всем отрезке задания определяется четырьмя коэффициентами, то для его полного построения на всем отрезке задания 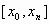 необходимо найти всего необходимо найти всего 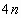 чисел. чисел.
Для выполнения третьего условия достаточно потребовать непрерывность сплайна во всех внутренних узлах
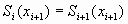 , , 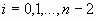
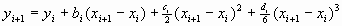
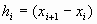
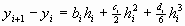 , ,
а также его первой
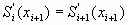 , , 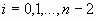
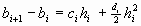
и второй производных в этих узлах
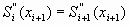 , , 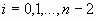
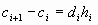
Вместе с первым требованием
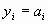 , , 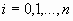
получается 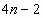 неравенства. неравенства.
Из вышеприведенных уравнений получается следующая система линейных уравнений:
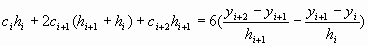 , , 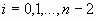 , ,
которую можно решить методом прогонки (см. “Системы линейных уравнений”).
Недостающие два условия можно получить, задав значения вторых производных на концах отрезка 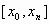 . .
Граничные условия первого типа. Задание на концах отрезка 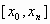 значений первой производной искомой функции: значений первой производной искомой функции:
|
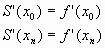
|
(1) |
Граничные условия второго типа. Задание на концах отрезка 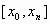 значений второй производной искомой функции: значений второй производной искомой функции:
|
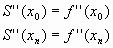
|
(2) |
Граничные условия третьего типа (периодические условия). Используются, когда интерполируемая функция является периодической с периодом 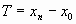 : :
|

|
(3) |
Граничные условия четвертого типа.
|
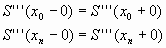
|
(4) |
Позволяют уменьшить число разрывов третьей производной во внутренних узлах 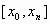 . .
В случае, если нет дополнительной информации о поведении аппроксимируемой функции, то используются естественные краевые условия (5), которые могут привести к резкому снижению точности аппроксимации вблизи концов отрезка 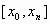 , т.к. вне интервала график представляет из себя прямую линию. , т.к. вне интервала график представляет из себя прямую линию.
|
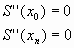
|
(5) |
|
|




