|
|
Деревья
Формально деревья можно определить как конечное множество A, состоящие из одного или более узлов таких, что: 1. имеется один узел, называемый корнем дерева, 2. остальные узлы (кроме корня) содержаться в m > 0 попарно не пересекающихся множествах A 1, . . . , Am, каждое из которых в свою очередь является деревом.
Деревья, как правило, дают хорошие представление о структуре отношения между элементами данных. Например, на рисунке показано дерево, представляющие формулу: (ab+cd)/bc.
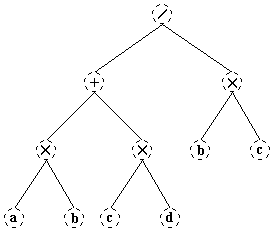
Один из классов деревьев следует выделить особо - это класс бинарных деревьев. Формально бинарное дерево - конечное множество узлов, которое либо пусто, либо состоит из корня и двух бинарных деревьев. Предыдущий рисунок пример дерева как раз такого класса.
При работе с деревьями часто приходится решать задачу обхода дерева. Для этого удобно использовать например такой рекурсивный алгоритм:
1. Корень дерева.
2. Если нет поддеревьев, то ВЫХОД,
иначе обходим все поддеревья слева направо.
|
|




