|
|
Ханойские башни
Головоломка "Ханойские башни" достаточно старая и хорошо известная, с ней связано несколько забавных легенд, но суть проблемы, которую я попытаюсь рассмотреть на примере данной задачи - использование рекурсивных алгоритмов и преобразование их к не рекурсивным.
Для начала сформулируем саму задачу. Даны три стержня ((н) - начальный, (к)- конечный, (д) - дополнительный) на стержень (н) нанизано некоторое количество дисков (будем полагать его равным n) при этом все диски имеют разный диаметр и расположены на стержне (н) в порядке уменьшения диаметра снизу в верх (см. рис).

Необходимо переместить все диски на стержень (к), т.е. головоломка должна быть приведена к виду:

при этом за один ход можно переместить только один диск, и в результате хода не должно возникнуть ситуации, когда диск с большим диаметром будет положен на диск с меньшим диаметром.

Итак, нам необходимо перенести n дисков со стержня (н) на стержень (к). Допустим у нас есть процедура перенесения n-1 диска, обозначим ее Х(n-1,(Ст1),(Ст2)), тогда задача легко разрешима для этого вначале перенесем n-1 диск со стержня (н) на стержень (д), применяя процедуру Х, затем перенесем n-ый диск со стержня (н) на стержень (к) (обозначим эту процедуру П((Ст1),(Ст2)) и наконец перенесем n-1 диск со стержня (д) на стержень (к). Работа выполнена . Алгоритм в этом случае можно записать следующим образом:
1. Х(n-1, (н), (д))
2. П((н),(к))
3. Х(n-1, (д), (к))
Теперь необходим частный случай, не являющийся рекурсивным. Если диск всего один, то можно сразу перенести его со стержня (н) на стержень (к), таким образом, выполняется тождество Х(1, (Ст1), (Ст2))=П((Ст1), (Ст2)). Таким образом, процедура Х представляется в виде блок-схемы:
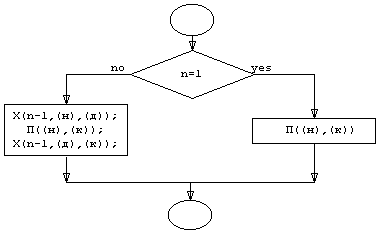
Вернемся к вопросу вычисления функции f(n). Для предъявленной рекурсивной процедуры, представление f(n) достаточно тривиально:
f(1)=1
f(n)=2* f(n-1)+1
Явный вид функции f(n) нетрудно найти из приведенных выше соотношений, пользуясь принципом математической индукции: f(n)=2 n -1.
Дополнительно к тому, что уже имеется, заметим еще одно свойство перемещаемых дисков. Пусть наши диски пронумерованы от 1 до n, таким образом, что диск с наименьшим диаметром имеет номер 1, второй по величине диаметра диск номер 2, и т.д., наконец диск с наибольшим диаметром имеет номер n. Тогда можно заметить, два диска с номерами одинаковой четности никогда не будут лежать друг на друге (т.е. диск с номером 2 не ляжет на диск с номером 4, 6 или 8). Докажем что это свойство выполнено. Доказательство будем проводить по индукции, допустим, что свойство выполнено для процедуры Х(p,(Ст1),(Ст2)), где p < n (для p=1 и Х(1,(Ст1),(Ст2)) свойство выполнено автоматически), далее докажем, что тогда свойство выполняется и для Х(n,(Ст1),(Ст2)). Начнем с переноса (n-1) дисков на стержень (д). Пока не передвинут (n-1)-ый диск, ни один диск не кладется непосредственно на диск с номером n и значит требуемое свойство выполнено. Рассмотрим момент, когда n-2 дисков находятся на одном стержне , диски с номерами n-1 и n - на другом стержне, а третий стержень пуст. Мы перемещаем диск с номером n-1. Теперь нужно переместить первые n-2 дисков на диск с номером n-1, поэтому диски будут оказываться на диске с номером n. Если мы помещаем диск с номером k на диск с номером n, то для того, чтобы образовать пирамиду дисков с номерами от k до 1 и иметь возможность, переместить диск с номером k+1 на диск с номером n-1. Но поскольку требуемое свойство выполняется для n-1 дисков, то честность k+1 диска не может совпадать с четностью n-1. А значит, она совпадает с четностью n, и отсюда следует, что четность n и k различна.
|
|




