Общие положения
Афинные преобразования находят широкое применение при решении задач компьютерной графики. Для этого геометрические объекты представляются в однородных координатах.
Однородным представлением n-мерного объекта является его представление в (n+1)-мерном пространстве, полученное добавлением еще одной координаты - скалярного множителя (или масштабного фактора). Таким образом точка на плоскости представляется тремя координатами (x,y,1).
Основной целью введения однородных координат в компьютерной графике является их удобство в применении: к геометрическим преобразованиям, для описания задач проективной геометрии и в связи с необходимостью описывать несобственные (бесконечно удаленные) точки пространства. При помощи троек однородных координат и матриц третьего порядка можно описать любое афинное преобразование плоскости.
Афинное преобразование является комбинацией линейных преобразований, сопровождаемых переносом изображений. Для афинных преобразований транспонированный последний столбец обобщенной матрицы 3х3 равен ¦0 0 1¦ .
Элементы произвольной матрицы афинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному описанию геометрического преобразования необходимо сложное преобразование разбить на ряд частных и для каждого из них найти соответствующую матрицу. Матрица общего преобразования определяется произведением матриц частных(элементарных) преобразований.
Матрица линейного преобразования общего вида для двумерных однородных координат выглядит следующим образом:
T = 
Учитывая влияние элементов матрицы на результат линейного преобразования, матрицу можно разбить на 4 подматрицы : 2х2, 1х2,2х1 и 1х1 ( смотри предыдущий рисунок), элементы которых выполняют следующие преобразования:
1) Элементы a, b, c, d верхней подматрицы 2х2 изменяют масштаб изображения, а также выполяют операции сдвига и вращения.
2) Элементы m, n подматрицы 1х2 выполняют операцию смещения (переноса) изображения.
3) Элементы p, q подматрицы 2х1 используются для получения проекций.
4) Элемент s подматрицы 1х1 осуществляет однородное изменение масштаба: если s<1, то происходит увеличение масштаба; если s>1, то происходит уменьшение масштаба.
Цепочка преобразований
Для выполнения более сложных преобразований необходимо определить цепочку основных (элементарных) преобразований, применяемых последовательно. В этом случае матрица сложного преобразования ищется в виде произведения матриц преобразований, составляющих цепочку.
Например, операция поворота изображения на угол "ф" в точке А=(m,n) выполняется в три этапа
:
1) Перенос точки вращения в начало координат.
2) Вращение изображения вокруг начало координат на угол "ф".
3) Обратный перенос точки вращения в прежнее положение.
Матрица полного преобразования Т определяется произведением матриц вышеперечисленных элементарных (частных) преобразований и равна:
Т =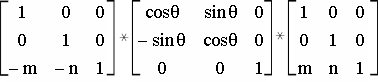
= =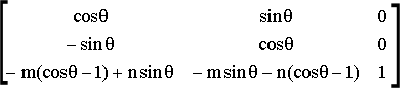
Заметим, поскольку операция умножения матриц не является коммутативной, в цепочке преобразований менять местами матрицы нельзя !




