|
|
Метод Гаусса
Данный метод предназначен для решения СЛУ из 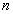 уравнений с уравнений с 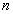 переменными. переменными.
Метод Гаусса состоит из двух этапов:
- прямой ход;
- обратный ход.
Прямой ход заключается в преобразовании исходной матрицы коэффициентов 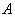 к верхней треугольной матрице и всей СЛУ – к треугольной СЛУ. к верхней треугольной матрице и всей СЛУ – к треугольной СЛУ.
Схема единственного деления (схема Гаусса)
Шаг 1. Счетчик циклов i устанавливается в единицу.
Шаг 2. Выбирается уравнение с наибольшим по абсолютному значению ненулевым коэффициентом при 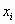 , у которого коэффициенты при , у которого коэффициенты при 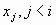 равны нулю. Если такого уравнения нет, то система может быть неопределенной совместной или несовместной и алгоритм заканчивает работу. Если номер выбранного уравнения отличен от i, то оно меняется с i-ым уравнением. равны нулю. Если такого уравнения нет, то система может быть неопределенной совместной или несовместной и алгоритм заканчивает работу. Если номер выбранного уравнения отличен от i, то оно меняется с i-ым уравнением.
Шаг 3. Уравнение i делится на 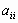 и из уравнений (i+1,n) исключается переменная и из уравнений (i+1,n) исключается переменная 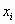 . .
Шаг 4. Счетчик i увеличивается на единицу. Если i меньше n, выполняется переход на шаг 2, иначе, прямой проход заканчивается.
Матричная запись схемы единственного деления
Обратный проход рассмотрен выше.
Схема Гаусса применяется также для вычисления определителя и нахождения обратной матрицы.
|
|




