|
|
Графы
Неориентированный конечный граф (граф) G – пара множеств (V,E), где V – непустое конечное множество вершин, а E – множество неупорядоченных пар различных вершин.
|V| – число вершин графа G.
E – множество ребер графа. |E| – число ребер графа G.
Геометрическая (графическая) интерпретация графа G=(V,E), где множество вершин V={a,b,c,d,e}, а множество ребер E={(a,c),(a,d),(b,d),(c,d)}, приведена на рис.1.
Рис.1. Неориентированный конечный граф.
Ориентированный конечный граф (орграф) G* – пара множеств (V,E*), где V – непустое конечное множество вершин, а E* – множество упорядоченных пар различных вершин.
|V| – число вершин графа G*.
E* – множество дуг графа. |E*| – число дуг графа G*.
Синоним понятия "вершина" – "узел".
Дуга – ориентированное ребро.
Геометрическая (графическая) интерпретация орграфа G*=(V,E*), где множество вершин V={a,b,c,d}, а множество дуг E*={<a,c>,<d,c>,<d,a>,<b,a>}, приведена на рис.2.
Рис.2. Ориентированный конечный граф.
Смешанный граф – граф, содержащий как ребра, так и дуги.
Ребра смешанного графа представляются парой противоположно направленных дуг (или биориентированной дугой), следовательно, смешанный граф преобразуется в орграф (рис.3).
|
1 2 |
|
Рис.3. |
1 - Смешанный граф. |
| |
2 - Ориентированный граф с противоположно направленными дугами. |
При преобразовании смешанного графа (рис.3.1) в орграф (рис.3.2) ребро (a, d) представляется парой дуг <a,d> и <d,a>, а дуги <a,c>, <c,d> и <b,d> остались без изменений.
Аналогично граф можно преобразовать к орграфу.
Взвешенный граф – граф, каждому ребру которого сопоставлено какое-либо значение, называемое весом ребра (рис.4).
Рис.4. Взвешенный граф.
Взвешенный орграф – орграф, каждой дуге которого сопоставлено какое-либо значение, называемое весом дуги.
Подграф графа G – граф 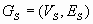 , где , где 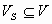 , , 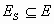 (рис.5). (рис.5).
Остовный подграф GS графа G – подграф GS, у которого 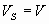 (рис.5.1). (рис.5.1).
|
1 2 |
|
Рис.5. |
1 - Граф. |
| |
2 – Один из остовных подграфов. |
Нуль-граф – граф, если 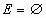 ( (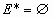 ). ).
Тривиальный граф – граф, состоящий из одной вершины 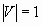 . .
Петля – ребро (дуга), у которого начальная вершина и конечная вершина совпадают (рис.6).
|
|
|
Рис.6. Петля. |
Мультимножество – множество, элементы которого могут встречаться в нем несколько раз. Кратность элемента – количество экземпляров элемента в мультимножестве.
Кратные ребра (кратные дуги) соединяют одну и ту же пару вершин.
Мультиграф – граф, у которого могут быть кратные ребра (рис.7).
Мультиорграф – орграф, у которого могут быть кратные дуги.
Ребра в мультиграфе задаются мультимножеством E, а дуги в мультиорграфе – мультимножеством E*.
|
|
|
|
|
Рис.7. Мультиграф. |
Рис.8. Псевдограф. |
Рис.9. Простой псевдограф. |
Псевдограф – граф, у которого могут быть кратные ребра и/или петли (рис.8).
Псевдоорграф – орграф, у которого могут быть кратные дуги и/или петли.
Простой псевдограф – граф, у которого могут быть петли (рис.9).
Простой псевдоорграф – орграф, у которого могут быть петли.
Примечание: в графе (орграфе) не может быть ни кратных ребер (дуг), ни петель.
|
1 2 |
|
Рис.10. |
1 – Полный граф. |
| |
2 – Полный простой псевдограф. |
Полный граф (полный орграф) – граф (орграф), если 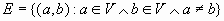 ( (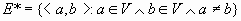 ) (рис.10.1). ) (рис.10.1).
Полный простой псевдограф (полный простой псевдоорграф) – граф (орграф), если 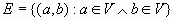 ( (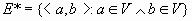 ) (рис.10.2). ) (рис.10.2).
Концевые вершины – вершины, определяющие ребро (дугу).
Для дуги первая вершина упорядоченной пары называется началом дуги (дуга “исходит” из вершины), а вторая вершина упорядоченной пары – концом дуги (дуга “заходит” в вершину). Для дуги < a,c> (рис.2) концевые вершины – вершины a и c, причем вершина a – начало дуги, а вершина c – конец дуги.
Смежные вершины – вершины, соединенные ребром (дугой).
Например, для орграфа на рис.2 вершины a и c – смежные вершины, а вершины a и b – нет.
Полный граф – граф, в котором каждая пара вершин смежная.
Полный орграф – орграф, в котором каждая пара вершин смежная.
Инцидентность ребра (дуги) и вершины – если вершина является концом ребра (дуги), то вершина инцидентна ребру (дуге) .
Например, для орграфа на рис.2 вершина a и дуга <a,c> – инцидентные, а вершина a и дуга <d,c> – нет.
Смежные ребра (дуги) – ребра (дуги), инцидентные одной вершине.
Например, для орграфа на рис.2 дуги < a,c> и <d,c> – смежные, а дуги <d,c> и <b,a> – нет.
Висячая вершина (лист) – вершина, инцидентная одному ребру (одной дуге).
Например, для орграфа на рис.2 вершина b – висячая вершина.
Изолированная вершина графа (орграфа) – вершина, не инцидентная ни одному ребру (ни одной дуге).
Например, для орграфа на рис.3.1 вершина e – изолированная вершина.
Изолированная вершина простого псевдографа (простого псевдоорграфа) – вершина, не инцидентная ни одному ребру (ни одной дуге), кроме петли.
Степень вершины – количество ребер (дуг), инцидентных данной вершине.
Петля увеличивает степень вершины на 2.
Полустепень захода вершины – количество дуг, заходящих в вершину.
Петля увеличивает полустепень захода вершины на 1.
Полустепень исхода вершины – количество дуг, исходящих из вершины.
Петля увеличивает полустепень исхода вершины на 1.
Степень вершины орграфа = полустепень исхода + полустепень захода.
Например, для орграфа на рис.3.2 полустепени исхода и захода, а также степень вершины приведены в таблице 1.
Таблица.1. Полустепени и степень вершин графа на рис.3.2.
|
Вершина |
Полустепень исхода |
Полустепень захода |
Степень |
Дополнительно |
|
a |
2 |
1 |
3 |
|
|
b |
1 |
0 |
1 |
Источник, лист |
|
c |
1 |
1 |
2 |
|
|
d |
1 |
3 |
4 |
|
|
e |
0 |
0 |
0 |
Изолированная вершина |
Изолированная вершина графа (орграфа) – вершина, степень которой равна нулю.
Источник – вершина орграфа, полустепень захода которой равна нулю.
Сток – вершина орграфа, полустепень исхода которой равна нулю.
Степень висячей вершины (листа) равна единице.
Рис.11. Сеть.
Сеть – взвешенный орграф с различными одним источником и одним стоком (рис.11).
|
|




