Для получения проекции объекта на картинную плоскость необходимо провести через каждую его точку прямую из заданного проектирующего пучка (собственного или несобственного) и затем найти координаты точки пересечения этой прямой с плоскостью изображения. При параллельном проектировании центр (несобственного) пучка считается лежащим в бесконечности (рис.1).

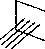


Рис. 1
Важное замечание.
Использование для описания преобразований проектирования однородных координат и матриц четвертого порядка позволяет упростить изложение и зримо облегчает решение задач геометрического моделирования.
При ортогональной проекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей (рис.2). Матрица проектирования вдоль оси
X на плоскость YZ имеет вид:
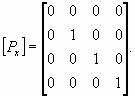
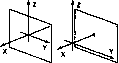
Рис. 2
В случае, если плоскость проектирования параллельна координатной плоскости необходимо умножить матрицу [Рх] на матрицу сдвига. В результате получаем
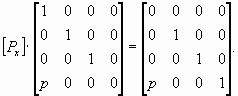
Аналогично записываются матрицы проектирования вдоль двух других координатных осей:
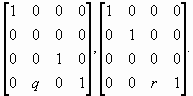
Замечание.
Все три полученные матрицы проектирования вырожденны.




