|
|
Перспективная проекция
Матрица соответствующего п epспективного преобразования (без проектирования) имеет следующий вид:
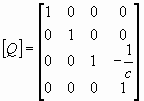
Обратим внимание на то, что последняя матрица не вырождена.
Рассмотрим пучок прямых, параллельных оси Z, и попробуем разобраться в том, Что с ним происходит под действием матрицы [Q].
Каждая прямая пучка однозначно определяется точкой (скажем, M(x, у, z)) своегo пересечения с плоскостью XY и описывается уравнениями X = x, Y = у, Z = t. Переходя к однородным координатам и используя матрицу [Q], получаем
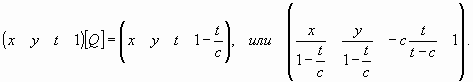
Устремим t в бесконечность.
При переходе к пределу точка ( x, у, t, 1) преобразуется в(0, 0, 1, 0). Чтобы
убедиться в этом, достаточно разделить каждую координату на t:
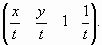
Точка (0, 0, -с, 1) является пределом (при t, стремящемся к бесконечности) правой части рассматриваемого равенства.
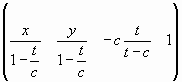
Тем самым бесконечно удаленный (несобственный) центр (0, 0, 1, 0) пучка прямых, параллельных оси Z, переходит в точку (0,0, -с, 1) оси Z.
Вообще каждый несобственный пучок прямых (совокупность прямых, параллельных заданному направлению), не параллельный картинной плоскости,
X = x + lt,Y = y + mt,Z = z + nt,n!=0,
под действием преобразования, задаваемого матрицей [Q], переходит в собственный
пучок
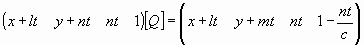
Центр этого пучка называют точкой схода.
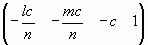
Принято выделять так называемые главные точки схода, которые соответствуют
пучкам прямых, параллельных координатным осям
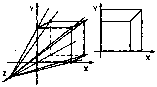
Рис. 9.22
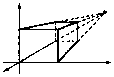
Для преобразования с матрицей [Q] существует лишь одна главная точка схода (рис. 9.22). В общем случае (когда оси координатной системы не параллельны плоскости экрана) таких точек три.
Матрица соответствующего преобразования выглядит следующим образом:
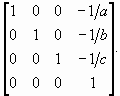
Пучок прямых, параллельных оси
0X 0Y
(1 0 0 0) (0 1 0 0)
переходит в пучок прямых с центром.
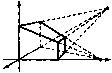
На рис. 9.23 изображены проекции куба со сторонами, параллельными координатным осям, с одной и с двумя главными точками схода

Точки (- a, 0, 0) и (0, -b, 0) суть главные точки схода.
|
|




