Приведем решаемую систему
Ax=b эквивалентным преобразованием к виду:
Это возможно сделать многими способами. Например, умножим слева обе части равенства
0 = -A x + b на произвольную невырожденную матрицу H и прибавим вектор x к правой и левой части полученного равенства:
x = x - H A x + H b = (E - H A) x + H b
Отсюда находим:
|
C є E - HA, d є H b. |
(1.12) |
Матрицу
H нужно выбирать так, чтобы C обладала определенными свойствами, о которых будет сказано ниже (теорема 1.1).
Итерационный процесс (то есть процесс последовательных приближений) метода простой итерации описывается формулой:
|
x(k+1) = C x(k) + d, k = 0, 1, ..., |
(1.13) |
где
x(0) - некоторое начальное приближение к решению (обычно полагают x(0)=d).
В координатной форме метод простой итерации записывается следующим образом:
x1(k+1) = c11x1(k) + c12x2(k) + ... + c1nxn(k) + d1
x2(k+1) = c21x1(k) + c22x2(k) + ... + c2nxn(k) + d2
...
xn(k+1) = cn1x1(k) + cn2x2(k) + ... + cnnxn(k) + dn
Таким образом
i-тая компонента (k+1)-го приближения к решению вычисляется по формуле
|
xi(k+1) = е nj=1 cijxj(k), i=1, ..., n |
(1.14) |
Имеет место следующая:
ТЕОРЕМА 1.1 Для сходимости последовательных приближений {
x(k)} метода простой итерации к точному решению системы (1.11) достаточно, чтобы || C || < 1.
Таким образом, если некоторая норма матрицы
C меньше единицы, то итерационный процесс, основанный на формуле (1.13), гарантированно сходится к искомому решению при любом начальном приближении x(0).
ЗАДАЧА 1.1
Доказать, что если матрица A обладает свойством
|aii| >е nj = 1, j № i|aij|, i = 1, ..., n,
то к неравенству ||
C ||Ґ < 1 для C из формулы (1.12) приводит матрица
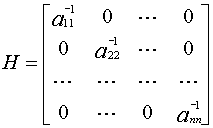
ТЕОРЕМА 1.2
Пусть || C || < 1, тогда при использовании метода простой итерации справедлива следующая оценка:
|
|| x - x(k+1) || ≤ || C || || x(k+1) - x(k) || / (1-|| C ||) |
(1.15) |
ДОКАЗАТЕЛЬСТВО
: Из равенств
x = Cx + d,
x(k+1) = C x(k) + d
путем вычитания получим
|
x - x(k+1) = C ( x - x(k) ). |
(1.16) |
Перенесем
x(k+1) вправо и вычтем вектор x(k) из левой и правой части полученного равенства:
x - x(k+1) = x(k+1) - x(k) + C (x - x(k)).
Теперь будем оценивать норму вектора
x-x(k+1) пользуясь неравенством треугольника и определением согласованности норм:
|| x - x (k) || ≤ || x (k+1) - x (k) || + ||C|| || x - x (k) ||.
Отсюда получаем оценку:
|
|| x - x(k) || ≤ || x(k+1) - x(k) || / (1-|| C ||) |
(1.17) |
Кроме того из (1.16) следует:
|| x - x (k+1) || ≤ || C || || x - x (k) ||.
Учитывая (1.17), окончательно получаем:
|| x - x(k+1) || ≤ || C || || x(k+1) - x(k) || / (1-|| C ||)
Теорема доказана.
Эта теорема позволяет сформулировать следующее условие окончания итерационного процесса при достижении задaнной точности
e:
|
|| x(k+1) - x(k) || ≤ (1-|| C ||) e / || C || |
(1.18) |
Действительно, в этом случае из теоремы 1.2 следует:
|
|| x - x (k+1) || ≤ e. |
(1.19) |
При выполнении неравенства (1.18) решение системы
A x = b полагают равным x(k+1) (с точностью e).
Из формул (1.15), (1.18) также видно, что чем меньше норма ||
C ||, тем быстрее сходимость итераций к решению.




