|
|
Системы линейных уравнений
Линейное уравнение (л.у.) – уравнение вида
|
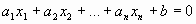
|
(1) |
|
где 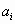 – числа, называемые коэффициентами л.у., – числа, называемые коэффициентами л.у., 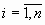 , ,
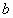 – число, называемое свободным членом л.у. – число, называемое свободным членом л.у.
|
|
Система линейных уравнений (СЛУ) – система вида
|
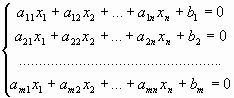
|
(2) |
|
где 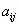 – числа, называемые коэффициентами СЛУ, – числа, называемые коэффициентами СЛУ, 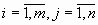 , ,
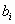 – числа, называемые свободными членами СЛУ, – числа, называемые свободными членами СЛУ, 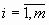 , ,
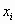 – переменные СЛУ, – переменные СЛУ, 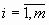 , ,
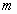 – количество уравнений СЛУ, – количество уравнений СЛУ,
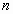 – количество переменных СЛУ. – количество переменных СЛУ.
|
|
Сокращенная форма записи СЛУ (2)
|
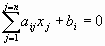 , , 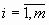 . .
|
(3) |
Матричная форма записи СЛУ (2)
|
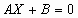
|
(4) |
|
где 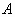 – матрица коэффициентов СЛУ размерности – матрица коэффициентов СЛУ размерности 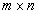 , ,
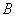 – вектор свободных членов СЛУ размерности – вектор свободных членов СЛУ размерности 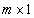 , ,
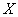 – вектор переменных СЛУ размерности – вектор переменных СЛУ размерности 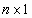 , ,
0 – нуль-вектор размерности 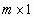 . . |
|
Квадратная СЛУ – СЛУ, состоящая из n уравнений с n переменными.
Решение СЛУ с n переменными – упорядоченная совокупность чисел 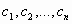 ( (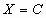 для(4)), являющихся решением каждого из уравнений, входящих в систему. для(4)), являющихся решением каждого из уравнений, входящих в систему.
1. Точные методы решения – методы решения, дающие точное решение задачи за конечное число арифметических и логических операций в предположении отсутствия округлений. Применяются для решения задач с малым числом переменных – не более 10 3.
2. Итеративные методы решения – методы решения, дающие возможность получить решение с заданной точностью или точное решение. Применяются для решения задач со средним числом переменных – не более 10 6. Требуют меньше вычислений, чем точные методы решения.
3. Вероятностные методы решения. Применяются для решения задач с большим числом переменных – более 10 6.
Совместная СЛУ – СЛУ, имеющая одно или несколько решений.
Определенная СЛУ – совместная СЛУ, имеющая единственное решение.
Неопределенная СЛУ – совместная СЛУ, имеющая более одного решения.
Несовместная СЛУ – СЛУ, не имеющая ни одного решения.
Однородная СЛУ (ОСЛУ) – СЛУ, все свободные члены которой равны нулю
1. Любая ОСЛУ имеет хотя бы одно решение – тривиальное решение, т.е. 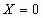 . .
2. Для того чтобы ОСЛУ имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был меньше количества переменных системы.
Неоднородная СЛУ (НСЛУ) – СЛУ, у которой хотя бы один свободный член отличен от нуля
|
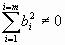 . .
|
(6) |
1. Для того чтобы НСЛУ была совместной СЛУ, необходимо и достаточно, чтобы ранг матрицы коэффициентов равен рангу расширенной матрицы (7).
2. Квадратная НСЛУ с вырожденной матрицей коэффициентов может быть совместной неопределенной системой или несовместной системой.
|
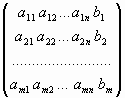 , ,
|
(7) |
|
где 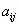 – коэффициенты СЛУ, – коэффициенты СЛУ, 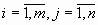 , ,
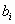 – свободные члены СЛУ, – свободные члены СЛУ, 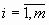 , ,
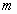 – количество уравнений СЛУ, – количество уравнений СЛУ,
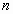 – количество переменных СЛУ. – количество переменных СЛУ.
|
|
Равносильные СЛУ – две СЛУ, множества решений которых совпадают.
1. Всякие две несовместные системы считаются равносильными.
Элементарные преобразования СЛУ :
- умножение некоторого уравнения системы на отличное от нуля число;
- прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число;
- перестановка местами двух уравнений системы;
- перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений.
Эквивалентные СЛУ – две СЛУ, полученные одна из другой с помощью элементарных преобразований.
1. Любые две эквивалентные СЛУ – равносильные.
2. Любая СЛУ приводится посредством элементарных преобразований к системе с трапециевидной матрицей.
3. Любая квадратная СЛУ с невырожденной матрицей коэффициентов A приводится посредством элементарных преобразований к системе с треугольной матрицей.
|
|




