Весьма широко на практике применяется итерационный метод Зейделя:
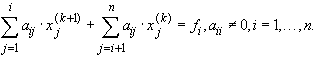
Компоненты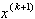 
находятся последовательно по формулам:
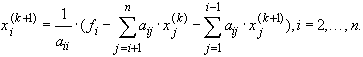
Запишем этот метод в матричной форме. Для этого представим матрицу A в виде суммы
,
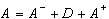где
, 
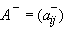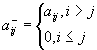- нижняя треугольная матрица,
, 
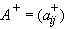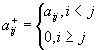- верхняя треугольная матрица.
В этих обозначениях метод Зейделя записывается следующим образом:
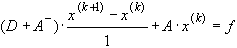
Исследуем сходимость метода Зейделя с помощью теоремы:
.
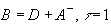В этом случае
,
,
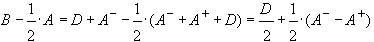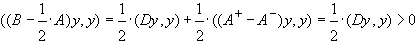если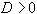 
. Следовательно, метод Зейделя сходится, если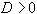
.
Неравенство 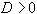следует из условия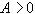 
.
Таким образом, метод Зейделя всегда сходится, если A - положительная матрица.
